在进行断点回归模型估计前后，需要对模型的稳健性进行检验。首先考察了解释变量密度分布的连续性来判断个体是否通过自选择操纵解释变量，进而改变自身是否接受处理的情况（Imbens，etal，2008）；其次进行了控制变量的连续性检验，即判断断点回归中其他特征变量或者控制变量在断点处是否平滑；然后进行添加控制变量的检验，即判断加入控制变量后断点回归结果是否仍然显著；最后进行安慰剂检验，即判断断点回归估计结果在其他假想临界值处的显著性。

（1）解释变量的连续性检验

解释变量的连续性假设是断点回归进行因果识别必须满足的前提条件。断点回归需要假定个体无法精确操控变量的指派，这就需要通过考察解释变量密度分布的连续性来实现（McCrary，2008）。因收集数据选择的是月度数据，样本的自选择问题容易表现为制造企业有机会通过推迟或修改发文时间，来提升改革政策的影响力度。采用McCrary核密度检验方法检验是否存在操纵解释变量时间的现象，图3-3给出了解释变量的密度分布图，可以看出，时间断点两侧密度函数的置信区间有很大部分重叠，没有出现显著的跳跃，这说明月度数据分布是连续且平滑的，故可认为时间断点两侧的密度函数不存在显著差异，即检验结果不存在内生分组。因此，可以认为断点附近不存在样本操纵解释变量的问题。

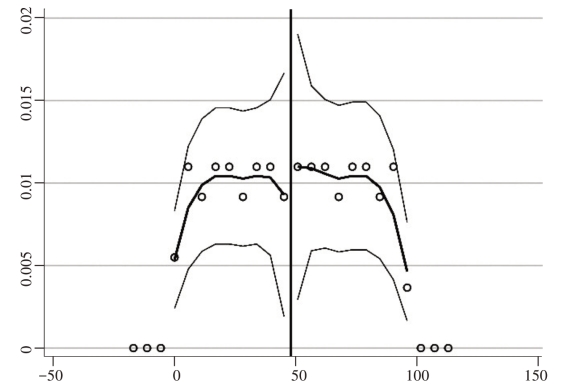
图3-3　政策时间断点处McCrary核密度检验

（2）控制变量的连续性检验

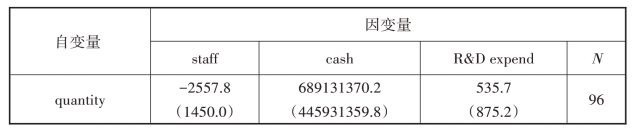
断点回归要求除政策因素外，对其他控制变量在断点处的连续性情况进行检验，结果如表3-5所示。各协变量在回归模型下的断点处均无显著跳跃，符合断点回归模型的要求。

表3-5　各协变量在断点处的跳跃情况

(www.daowen.com)

（3）添加控制变量的检验

表3-4中的模型汇报了加入控制变量后断点回归的估计结果，结果显示在加入控制变量后供给侧结构性改革政策对我国制造企业的改革意愿仍保持显著影响。因此，可以判定添加控制变量对本文的研究结果基本不存在影响。

（4）安慰剂检验

对断点回归模型进行证伪检验，具体检验标准如下：如果估计结果在其他假想的临界处是显著的，那么则可推测原断点回归模型的估计结果不太可信；如果估计结果在其他假想临界处并不显著，则认为原断点回归模型结果较为可靠。因此，在原政策断点的前后时间中随机选择了4个断点，即2013年2月、2015年2月、2017年2月和2019年2月。

表3-6　基于其他假设断点的回归估计

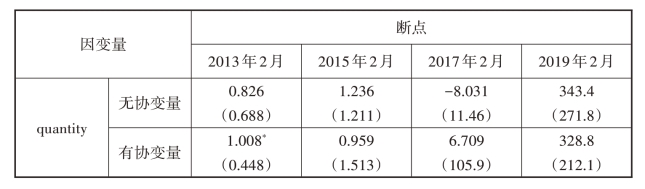
注：1.括号中是经异方差和序列相关修正后的标准差；
2.*、**、***分别代表显著性水平为10％、5％、1％；
3.表3-6中的局部效应量是基于三角内核非参数方法获得的，且是采用最优带宽时的估计值。

根据以上两种回归分析结果，接受假设H，即国家供给侧结构性改革政策颁布后，制造企业改革的“发文数量”有明显提升，说明受政策影响，制造企业供给侧结构性改革意愿有明显提升，表明国家政策对制造企业进行供给侧结构性改革有引导作用。

在我国供给侧结构性改革政策背景下，本课题对制造企业供给侧结构性改革意愿进行了分析，应用网络爬虫技术获得了样本数据，对我国制造企业供给侧结构性改革意愿的强度进行了测量，并构建了政策对制造企业供给侧结构性改革意愿影响的断点回归模型，进行了实证分析，研究的实证结果表明，供给侧结构性改革政策对我国制造企业的改革意愿具有正向影响，并且解释变量的连续性检验、控制变量的连续性检验、添加控制变量的检验和安慰剂检验的结果都表明本文的断点回归模型具有稳健性。因此，可以得出供给侧结构性改革政策对制造企业供给侧结构性改革意愿提升有显著促进作用，另外，意愿的测量方法，对今后相关研究具有借鉴和启发意义。