城市会不会、该不该出现，为什么会出现，在何处出现，当前城市规模太大还是太小，是否能够持续下去以及城市规模受哪些因素影响等一系列问题，一直是城市经济学关注的热点问题，也是新经济地理学家积极探究的问题。阿诺特（Arnott，1979）的最优城市规模空间理论建立在住宅区位理论的基础之上，通过经济总量之间的关系来研究最优城市规模的必要条件。亨德森（Henderson ，1974）讨论了在什么样的情形下均衡规模与最优规模将会不同。他将最优规模定义为社会计划者最大化经济中参与者的潜在福利而导致的城市规模，均衡城市规模则由劳动者的区位决策和资本所有者的投资决策决定，二者都试图最大化他们各自的福利。在两城市经济中，阿纳斯（Anas，1992 ）在推导出效用与人口规模的倒U形关系后，证明了当旧城市太大时，需要许多个体集体迁移到新城市，但是在旧的大城市极端拥挤前，先搬到新城市的少数人总要吃亏。因此，在放任自由的经济里，新城市总是诞生得太迟。贝特南里和布莱克（Bertinelli and Black， 2004）考察了最优城市规模和均衡城市规模，发现在没有移民限制的情况下，城市将会变得太大。克鲁格曼（Krugman，1991）研究表明，城市的最大规模如何受限于规模经济、运输成本、人口密度以及制造业就业人口比例。阿德斯和格莱泽（Ades and Glaeser， 1995）发现独裁政治下的中心城市比民主政治下的中心城市平均规模大50%。布莱克和亨德森（Black and Henderson， 1999， 2003）发现不同的城市类型有不同的绝对规模，一个城市产业构成的变化改变了城市的相对规模。杜兰顿和普加（Duranton and Puga， 2004）分析认为，有效的城市规模随通勤成本的增加而下降，随集聚收益递增程度的提高而上升。欧和亨德森（Au and Henderson， 2006）利用中国1997年的205个城市的数据进行的回归分析表明：在中国205个城市中，只有10%的城市其规模超过最优规模，而大部分城市的规模低于最优水平。

近年来，国内许多学者对我国最优城市规模进行了许多有益的理论探讨和实证考察。蒋涛和沈正平（2007）结合规模收益递增和单中心城市模型，分析了通勤成本、城市规模收益递增程度对最优城市规模的影响。他们发现在一定条件下，城市人均收入与城市规模之间存在倒U形关系。张应武（2009）利用2002-2006年间我国285个地级及以上城市数据估计了我国城市的最优规模和城市规模分布函数，研究表明，中国城市发展的最优规模为500万人。 肖文和王平（2011）在新经济地理模型框架下，研究认为外部性对城市发展有重要影响。他们通过数值模拟发现：福利水平与城市规模之间表现出倒U形关系；刘永亮（2011）认为，从整体上看，中国目前不存在过度规模城市，限制大城市规模的观点依据不足。武彦民和杨峥（2012）采用1999-2009年31个省面板数据对中国城市成本收益模型进行了计量分析，结果表明全国26个省低于估算的最优城市人口密度，验证了中国存在城市面积的扩张与人口的增加不协调发展的情况。以上模型存在的不足有：虽然有理论基础，但结果靠数值模拟；过度依赖计量经济模型；用人均收入代替福利水平研究城市的最优规模。总之，没有一个空间经济理论模型做基础。

作为第三章所建立的基本模型的一个理论应用，本节研究城市的最优规模是否存在，在什么条件下存在，有哪些因素会影响城市的最优规模。

现在通过最大化（4.14）式的间接效用函数，决定最优城市规模，即间接效用函数对r求导：

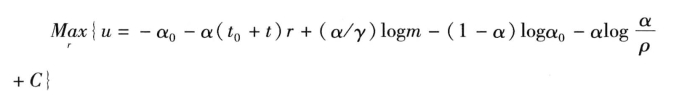
我们计算r的一阶和二阶条件。一阶条件是du/dr = 0 。

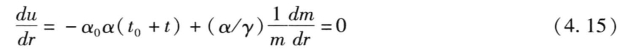
根据（3.24）式，有：

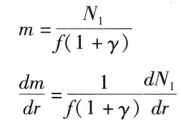
所以一阶条件转化为：

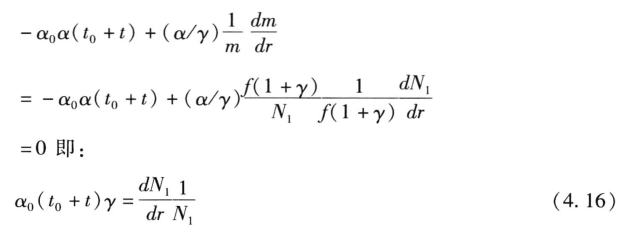
根据（4.14）和（4.16）有：

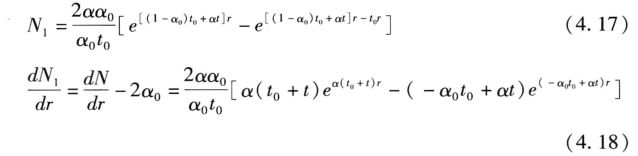
将（4.17）和（4.18）两个方程联系起来得到：

将（4.19）代入（4.16）有：

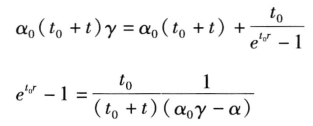
解得最优城市规模如下：(www.daowen.com)

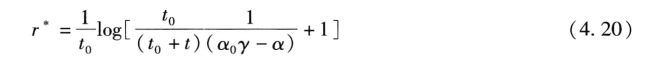
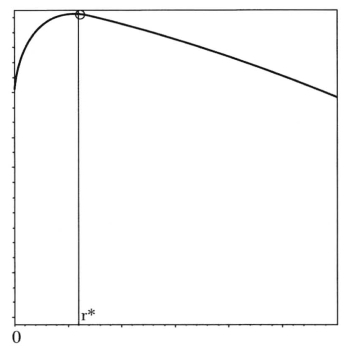
图1.1　城市均衡效用与城市规模的关系

现在分析影响最优城市规模的因素。从（4.20）可以看出，最优城市规模取决于农产品和工业品的运输因子、消费者在农产品和工业品上的支出比例以及消费者对工业品多样化的偏好。工业品的运输因子越大，最优城市规模就越小，否则运输到城市外围的工业品价格非常高。消费者在农产品上的支出比例越大，最优城市规模也越小。而消费者在工业品上的支出比例越大，最优城市规模将越大。这是因为农业部门是分散在城市外围的，而制造业部门是完全集中在城市中心的。消费者对工业品多样化的偏好越大，最优城市规模越大，因为城市规模越大，意味着工业品品种越多。根据我们对最优城市规模的定义，并从图1可以看出，如果r = r*，这个城市的代表性消费者将会获得最大的效用水平。如果r ＜ r * ，城市可以进一步集聚，消费者的效用水平将随着人口的增加而提高。如果r ＞ r * ，这个城市的人口过于集中，人口集聚带来的工业品价格下降和品种增多的好处被城市中心工人工资的下降抵消掉。城市人口的进一步集聚，只能带来消费者效用水平的下降。相应地，根据（4.7），最优的城市人口规模也决定了，N*=N（r* ）。

为了表明从一阶条件得到的城市规模的解确实是最大值^[1]，我们分析二阶条件。如果二阶条件d2 u/dr2 ＜ 0，那么以上求解得到的城市规模就是最优城市规模。

根据（4.15）可得：

其中为常数。

命题：对于任何A和B，A+B＞0，A＞0，定义h（r）=eA+Br-eBr，那么：

（ⅰ）h（r）是r的增函数，或h′（r）≥0

（ⅱ）h″（r）可能是正的或负的。

（ⅲ） ［h′（r） ］2-h″（r）h（r） ＞0

根据这一命题，因此有：

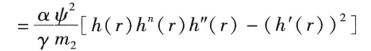
应用附录二中的命题有：

至此，我们已经证明，最优城市规模存在且是唯一的。