在上述推导中，把一个城市看成一个点，所以考虑的是城市中心的消费。现在考虑一个生活在离城市中心距离为y的农业消费者。

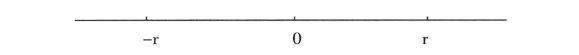
图1.1　单个城市的内部空间结构

线性城市，长度为2r，城市中心为0，城市中心两边是对称的，我们只需要考虑半径r为正的部分^[7]。

我们定义工业品的本地需求价格为p+，异地需求价格为p-。区分下标“+”和“-”很重要，因为在后面研究城市之间的运输成本时二者是不一样的。p+和p-是有效需求价格（或者说，如果有运输成本存在的话，是考虑运输成本之后的价格） ，p是供给价格（生产者在生产地的要价）。

定义代表性农产品和工业品的需求价格为p0（y）和p+ （y）。标准化p0（ 0）=p0=1 ，p+ （0） = p+。那么生活在y地的消费者（包括农业工人和地主）面临的农产品和工业品价格分别为：

注意在（3.10）和（3.11）中的符号是一正一负的，这是农产品和工业品在一个城市内不同的运输方向所致。农产品在城市外围生产^[8]，一部分农产品需要从外围运送到城市中心供制造业工人消费，由于存在运输成本，城市中心的农产品价格自然高于城市外围的农产品价格，即p+ （y）=p+etay ＞p+ （0）=p+。同样道理，工业品是在城市中心生产的，一部分工业品需要运送到城市外围供农业工人和地主消费，由于运输成本的存在，城市中心的工业品价格自然低于城市外围的工业品价格，即。当y充分大时，生活在y地的消费者面临的农产品价格趋于零，而工业品价格趋于无穷大。从中我们也可以看出，城市边界有一个软上限。

分析至此，我们可以看到：只有一个城市的时候，我们只需要考虑城市内部工业品和农产品的运输成本；当出现多个城市时，我们不仅要考虑城市内部工业品和农产品的运输成本，而且要考虑城市之间工业品交易的运输成本。

根据（3.8），一个位于区位y的劳动者将获得效用u（y） ：

(www.daowen.com)

利用（3.10）和（3.11），我们有：

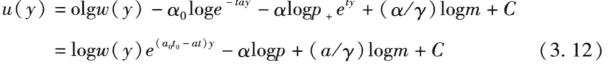
根据等效用原理，在均衡时，所有工人的效用水平是相同的，否则效用低的地方的消费者将搬到效用高的地方。首先，在不同区位上的农业工人是等效用的，生活在离城市中心越近的农业工人，其生产的农产品在运送到中心的过程中所损耗的越少，因此同时必须承担更高的地租；相反，生活在离城市中心越远的农业工人，其生产的农产品在运送到中心的过程中所损耗的相对越多，因此其在生产过程中承受的地租成本越低。地租和运输成本二者之间相互抵消、综合作用的结果导致不同地点的农业工人将获得相同效用的。如果效用不等，效用低的区位的农业工人会迁移到效用高的区位。其次，生活在城市中心的所有制造业工人都是等效用的。因为他们生活在同一个中心，工资相同，消费的产品的价格和可获得的品种相同，效用自然是一样的，这也可由文中得到的均衡效用函数可以看出。最后，均衡时，农业工人与制造业工人必须等效用。如果二者不是等效用的，那么就有农业工人或者制造业工人将选择改变自己的区位和工作类型。均衡的实现过程都是市场力量自发作用的过程，我们考察的是如何维持这种已有的均衡。一旦某种外生力量，比如人口增加、偏好变化、运输技术的改善，打破了这种均衡，那么城市原有结构将发生变化，从原有的单中心向多中心或者从单个城市向城市群、卫星城市演化，甚至退回到各个个体自给自足的社会，这是后面将要考虑的问题。

接下来我们需要通过对于在区位y的单位土地，农业企业利润为零推导w（r）。由于农产品的生产是在规模报酬不变的条件下利用一单位土地和单位劳动力生产的，所以农产品企业在单位土地上的产出收入为p0（y），这部分收入流向两个地方：支付给地主的土地租金和支付给工人的工资，即：

假设城市边缘的租金为0，推导得到城市中心的工人的工资：

利用前面推导得到位于城市中心的消费者的效用水平，可得：

这是任一消费者的间接效用函数，有三个内生变量：城市地理规模（r），工业品的供给价格（p）和工业品的规模（m）。给定城市人口规模N，所有这些变量将内生决定。