正式实验采用被试内设计，被试分别针对三种不同实验条件——决策收益者为自身、朋友和陌生人——完成包含混合型、收益型、损失型、检验型的150次风险决策。在本部分，我们将比较三种实验条件下，决策的反应时、决策者对风险选项的接受率以及损失厌恶的差异。

1.操纵检查

操纵检查作为数据分析的第一步，主要用来判断被试是否在社会距离不同的决策中都保证认真，以排除因注意力分配不同所导致的自我-他人决策行为差异（Barrafrem、Hausfeld，2019）。比方说：当决策收益人为自己时，被试所得与自己的决策行为直接相关，因此被试会认真对待相关决策，但是当决策收益人为陌生人或者朋友时，决策收益者的最终所得并不会对决策者的最终收益造成任何影响，所以被试没有动机在这两种决策条件中仍保持认真的态度。

操纵检查应用的数据为每种决策条件中的10个检验型决策试次。该10个决策试次随机分布在混合型、收益型、损失型三种决策类型中，并包含绝对占优的选项（如：风险选项为以50%概率得到30，以50%概率得到0，确定选项为确定得到50，所以确定选项为占优选项）。被试在三种决策条件下选择占优选项的数量均值均接近检验型决策试次总数10，具体均值为：

Mself=9.98，Mstranger=9.98，Mfriend=9.38，

标准差分别为：

SDself=0.65，SDstranger=0.91，SDfriend=1.39。

被试内重复测量ANOVA方差分析结果显示，三种决策条件下，选择占优选项的数量不存在显著差异（p＝0.306）。换言之，对检验型决策试次的分析表明，无论决策收益者的身份是谁，决策者在完成风险决策任务时的态度都是认真且无差的。

2.损失厌恶程度间接指标

（1）反应时

首先，我们剔除了反应时中的异常值（outlier）。针对每一种决策条件，我们计算了该条件下所有决策试次的反应时的均值和标准差，并将位于均值加减2倍标准差范围以外的反应时定义为异常值并在对反应时的分析中将其剔除。过长的反应时可能意味着注意力不集中，而过短的反应时则可能意味着决策时未经思考或键盘误按，因此予以剔除，从而保证反应时数据更能反映被试真实的思考时间。与预实验类似，在正式实验中我们也通过反应时热区图粗略比较被试对损益的敏感程度。在预实验中，我们绘制了关于绝对增（降）幅变化的反应时热区图，但由于正式实验中通过操纵乘子来产生不同的决策选项，因此反应时热区图也是根据乘子的变化来绘制的。从图形美观性以及分析难度的角度考虑，我们将乘子两两合并后进行分析。我们仍用颜色深浅来表示反应时长短，其中颜色越深表示反应时越长，颜色越浅表示反应时越短。在对反应时进行分析时，我们重点关注反应时最长的试次分布，在这些试次中被试对哪个选项感到难以抉择，就反映了被试选择风险选项和确定选项的决策边界。

此外，由于正式实验中包含三种不同的决策类型（检验型决策仅用来进行操纵检验，不进入其他分析），我们将对混合型、收益型、损失型风险决策类型对应的反应时结果分别进行汇报。

A.混合型决策

图12.6展示了混合型风险决策中，为自己（左）、朋友（中）和陌生人（右）决策时的反应时热区图。当决策收益者为自己时，决策边界出现在潜在损失为0.7~0.8倍于潜在收益的选项中；而在决策收益者为朋友时，表征决策边界的最长反应时对应0.9~1.0的乘子；在决策收益者为陌生人时，相应乘子为1.1~1.2。简而言之，随着社会距离的增加，与潜在收益效用相抵消的潜在损失值呈现增大趋势。这也在一定程度上说明，被试在混合型收益中，对潜在损失的敏感程度随社会距离的增加而降低。

图12.6　混合型风险决策中，不同社会距离下的决策反应时热区图

注：左、中、右三图分别代表为自己、朋友和陌生人进行决策。其中，颜色越深表示反应时越长，颜色越浅表示反应时越短，方框中的数据为平均反应时，单位为毫秒。
图片来源：作者绘制。

B.收益型决策

图12.7展示了收益型风险决策中，为自己（左）、朋友（中）和陌生人（右）决策时的反应时热区图。当决策收益者为自己时，决策边界出现在潜在收益为2.2~2.4倍于确定收益的选项中；而在决策收益者为朋友时，反映决策边界的最长反应时对应2.2~2.4的乘子；在决策收益者为陌生人时，潜在收益约2.0倍于确定收益时达到被试的决策边界。简而言之，在收益型决策中，决策者表现出对确定性收益的偏好，即风险规避的行为特征。但随着社会距离的增加，这种对风险规避的偏好出现了一定程度的减弱。

图12.7　收益型风险决策中，不同社会距离下的决策反应时热区图

注：左、中、右三图分别代表为自己、朋友和陌生人进行决策。其中，颜色越深表示反应时越长，颜色越浅表示反应时越短，方框中的数据为平均反应时，单位为毫秒。
图片来源：作者绘制。

C.损失型决策

图12.8展示了损失型风险决策中，为自己（左）、朋友（中）和陌生人（右）决策时的反应时热区图。当决策收益者为自己时，决策边界出现在潜在损失为2.0~2.4倍于确定损失的选项中。而在决策收益者为朋友和陌生人时，反映决策边界的最长反应时对应1.6~2.0的乘子。简而言之，在损失型决策中，决策者表现出对不确定性损失的偏好，即风险寻求的行为特征。但随着社会距离的增加，这种风险寻求的特征出现了一定程度的减弱。

图12.8　损失型风险决策中，不同社会距离下的决策反应时热区图

注：左、中、右三图分别代表为自己、朋友和陌生人进行决策。其中，颜色越深表示反应时越长，颜色越浅表示反应时越短，方框中的数据为平均反应时，单位为毫秒。
图片来源：作者绘制。

值得注意的是，为了增强图片的可读性，我们对乘子进行了归类合并，因而损失了关于某个具体乘子的反应时差异信息，这可能导致在损失型风险决策中，为自己和为他人决策时的决策边界在热区图中差别并不明显。

（2）风险选项接受率

在实验范式部分，我们已经对每种决策类型的乘子设置依据进行了阐述，并提出通过对被试风险选项接受率的分析可以粗略推断被试在该决策类型下的风险态度。所以，本部分将通过绘制折线图来反映不同风险决策类型中，风险选项接受率随乘子增大的变化趋势，比较社会距离对风险态度的影响。其中，风险选项接受率为某一乘子下，被试接受风险选项的数量与全部试次数量之比。接下来，我们将对混合型、收益型、损失型风险决策类型对应的风险选项接受率结果分别进行汇报。

A.混合型决策

如图12.9所示，在混合型风险决策中，风险选项接受率随乘子的增大而降低。并且，从整体上看，代表下一受试者（陌生人）的曲线位于代表朋友和决策者自身的曲线上方。朋友和决策者自身的曲线类似，但代表朋友的曲线所处位置略高。由此可见，为陌生人决策时的风险选项接受率总是高于为自己和朋友决策时。此外，与决策边界（风险选项接受率为50%时）所对应的乘子，在为陌生人决策时最大，其次是为朋友决策，而在为自己决策时最小，并且均小于使风险选项和确定选项相等的乘子1.0。这说明，从总体上看，决策者在混合型风险决策中表现出风险规避的行为特征，并且风险规避程度随着社会距离的增加而降低。这种风险规避的差异是由对损失敏感程度的不同导致的，面对同等大小的损失值，在为自己决策的实验条件下，需要用更大的收益值来弥补，才能达到选择“风险”和“确定”的决策边界。而在为陌生人决策的实验条件下，则不需要那么大的潜在收益值即可达到决策边界。基于上述分析，我们得出，在混合型风险决策中，决策者对损失的敏感程度随社会距离的增加而降低。

图12.9　混合型风险决策中，风险选项接受率随乘子变化情况(www.daowen.com)

图片来源：作者绘制。

B.收益型决策

如图12.10所示，在收益型风险决策中，风险选项接受率随乘子的增大而上升。而且，为自己决策时的风险选项接受率总是低于为朋友和陌生人决策时。此外，与决策边界（风险选项接受率为50%时）所对应的乘子，在为陌生人决策时最小，其次是为朋友决策，而在为自己决策时最大，并且均大于使风险选项和确定选项相等的乘子2.0。这说明，从总体上看，决策者在收益型风险决策中表现出风险规避的行为特征，并且风险规避程度随着社会距离的增加而降低。

图12.10　收益型风险决策中，风险选项接受率随乘子变化情况

图片来源：作者绘制。

C.损失型决策

如图12.11所示，在损失型风险决策中，风险选项接受率随乘子的增大而降低。而且，为自己决策时的风险选项接受率总是高于为朋友和陌生人决策时。此外，与决策边界（风险选项接受率为50%时）所对应的乘子，在为朋友和陌生人决策时小于为自己决策时，但三种实验条件下决策边界所对应的乘子总是不小于风险选项和确定选项相等的乘子2.0。这说明，从总体上看，决策者在损失型风险决策中表现出风险寻求的行为特征，并且风险寻求程度随着社会距离的增加而降低。

图12.11　损失型风险决策中，风险选项接受率随乘子变化情况

图片来源：作者绘制。

3.损失厌恶值的直接估计

从损失厌恶的间接指标（反应时、风险选项接受率），我们可以大致推断和比较决策者在不同决策条件下的风险态度与损失厌恶程度，但无论是反应时还是风险选项接受率都不能提供关于风险态度和损失厌恶的直观量化表达。基于此，我们将对预实验中的简化的线性效用模型进行优化，构建基于前景理论曲线型价值函数的结构模型，并用最大似然估计（maximum likelihood estimation，MLE）的方法来估计风险态度和损失厌恶值。

在结构模型中，决策者选择风险选项的概率被定义为（Rutledge et al.，2014；Rutledge et al.，2015）：

其中，μ代表了随机程度。Ugamble和Ucertain分别代表风险选项和确定选项的效用值，并可分别通过如下表达式进行计算：

其中，待估计的参数为风险态度参数α和损失厌恶参数λ。风险态度参数α＜1说明了效用函数在收益域是凹函数，而在损失域是凸函数。α的值越小意味着收益域的风险规避程度和损失域的风险寻求程度更高；α越趋近于1意味着风险态度越趋近于风险中性（Harrison，2008；Sokol-Hessner et al.，2009）。如果被试是损失厌恶的，则损失厌恶参数λ＞1；与之相反，如果被试是收益寻求（对收益比对等额损失更敏感）的，则损失厌恶参数λ＜1；而如果被试对收益和损失的敏感程度相同，则损失厌恶参数λ＝1（Harrison，2008；Köbberling、Wakker，2005）。为了比较不同决策条件下的风险态度参数α和损失厌恶参数λ的差异，模型还引入了虚拟变量来表达三种不同的决策条件。最后，通过在Stata 12中编写代码，我们采用最大似然估计方法估计三种决策条件下的风险态度参数α和损失厌恶参数λ的具体值。估计的结果如表12.4、表12.5所示，其中最右侧一列表示删去极端被试后的估计结果。极端被试在本实验中被定义为对所有决策试次都给予相同的按键选择的被试。

表12.4　对损失厌恶程度的估计结果（以为自己决策为参照组）

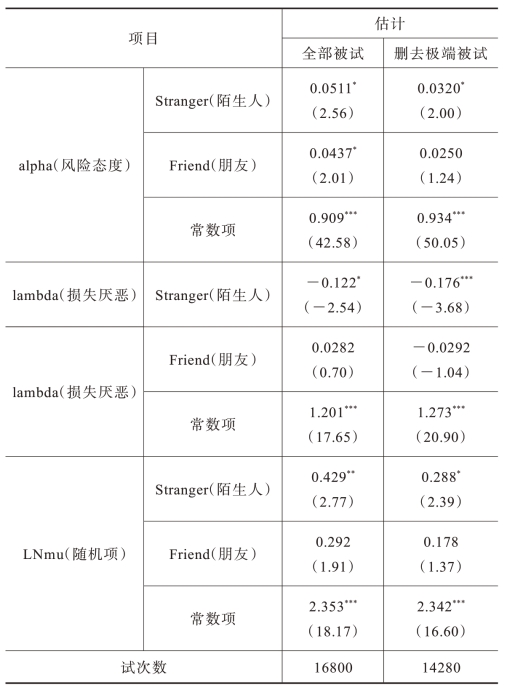
注：括号内为t值，*表示p＜0.05，**表示p＜0.01，***表示p＜0.001。
资料来源：作者整理。

表12.5　对损失厌恶程度的估计结果（以为陌生人决策为参照组）

注：括号内为t值，*表示p＜0.05，**表示p＜0.01，***表示p＜0.001。
资料来源：作者整理。

从表12.4、表12.5中可以看出，删除和不删除极端被试，对估计结果的大小和显著性影响不大。但是为了使结果更严谨和具有说服力，我们仅描述删除极端被试后的结果，并在结果讨论部分也仅对删除极端被试的结果进行讨论。

首先，风险态度参数α反映了决策者的风险态度，在三种实验条件下，决策者的α均小于1，这再一次验证了前景理论中所描述的“价值函数在收益域是凹函数，在损失域是凸函数”。并且，尽管最大似然估计结果仅证实了为自己和陌生人决策时α的显著差异，但我们仍能观察到α按照为自己、朋友、陌生人决策的顺序依次增大的趋势。

从回归结果中的损失厌恶参数λ我们可以看出，相比于为陌生人决策而言，为自己（见表12.5，以陌生人为参照组时，自己虚拟变量的系数是0.176）和为朋友（以陌生人为参照组时，朋友虚拟变量的系数是0.146）决策的损失厌恶参数λ显然更大。当比较为自己和朋友决策时的损失厌恶差异时，虽然我们仍然能观测到为自己决策时损失厌恶参数λ更大的趋势（以为自己决策为参照组时，朋友虚拟变量的系数为负），但该系数没有达到显著性水平。损失厌恶的绝对值及差异显著性见图12.12。

图12.12　不同社会距离下的损失厌恶估计值

注：*表示p＜0.05，**表示p＜0.01，***表示p＜0.001。
图片来源：作者绘制。

在整体层面观察到了损失厌恶差异的趋势后，我们对损失厌恶进行了基于个体层面的估计（表12.6）。排除无法迭代出结果的被试后，我们采用SPSS 20对估计值进行了被试内单因素方差分析（社会距离：自己vs朋友vs陌生人），统计结果显示社会距离的主效应显著［F（2，56）＝7.71，p＝0.001，η2＝0.22］。后续的配对样本t检验结果显示，损失厌恶参数λ在为自己决策时显著大于为陌生人决策时（t＝3.81，p＝0.001），且为朋友决策时的损失厌恶参数λ大于为陌生人决策时（t＝2.52，p＝0.018），但为自己与为朋友决策时的差异不显著（p＞0.05）。

表12.6　个人层面损失厌恶估计值的描述性统计

资料来源：作者整理。