该实验任务用Python编写，被试在实验过程中的重要行为数据，包括反应时、按键等都随着实验任务的进行而被记录下来，并保存在表格中。对行为数据的分析首先通过结构化模型直观估计不同社会距离下所表现出的损失厌恶参数值，从而量化地分析在反馈加工阶段，社会距离是否会影响损失厌恶。

对损失厌恶的估计方法与第十二章中的正式实验类似，但在本章中，我们对每个被试的损失厌恶参数进行估计，得到个人层面的损失厌恶参数值。其中，基于个人的损失厌恶参数计算公式为：

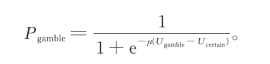
在公式中，μ代表了随机性程度，Ugamble和Ucertain分别代表风险选项和确定选项的效用值，并可分别通过如下表达式进行计算：

其中，待估计的参数为风险态度参数α和损失厌恶参数λ。风险态度参数α小于1说明效用函数在收益域是凹函数，而在损失域是凸函数。α的值越小意味着收益域的风险规避程度，以及损失域的风险寻求程度更高；α越趋近于1意味着风险态度越趋近于风险中性（Harrison，2008；Sokol-Hessner et al.，2009）。如果被试是损失厌恶的，则损失厌恶参数λ＞1；与之相反，如果被试是收益寻求（对收益比对等额损失更敏感）的，则损失厌恶参数λ＜1；而如果被试对收益和损失的敏感程度相同，则损失厌恶参数λ＝1（Harrison，2008；Köbberling、Wakker，2005）。我们通过在Stata 12中编写代码，采用最大似然估计方法估计每个被试在三种决策条件下的风险态度参数α和损失厌恶参数λ的具体值。

表14.1呈现对反馈加工阶段的损失厌恶估计值的描述性统计，结果显示：被试为自己决策时的损失厌恶估计值的变化范围为0.81~3.38，均值为1.27，标准差为0.53；为朋友决策时的损失厌恶估计值的变化范围是0.36~3.00，均值为1.17，标准差为0.50；为陌生人决策时的损失厌恶估计值的变化范围为0.18~1.94，均值为0.95，标准差为0.33。单因素方差分析（社会距离：自己vs朋友vs陌生人）的结果证明了社会距离的主效应［F（2，52）＝5.07，p＝0.01，η2＝0.163］。图14.3呈现了后续的两两配对t检验结果，为自己（t＝2.83，p＝0.009）和朋友（t＝-2.93，p＝0.007）决策时的损失厌恶估计值相较于为陌生人决策时更大，为自己和朋友决策时的损失厌恶估计值在趋势上存在差异，但并未达到显著性水平（p＞0.05）。

表14.1　基于反馈加工阶段中损失厌恶估计值的描述性统计(www.daowen.com)

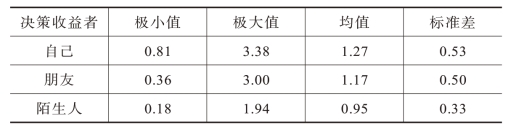
资料来源：作者整理。

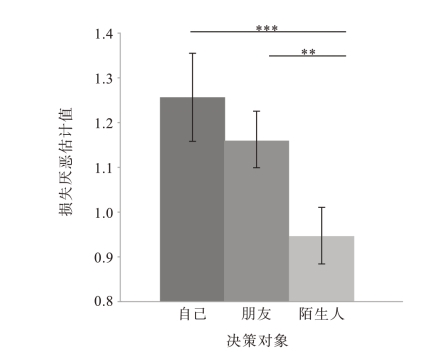
图14.3　决策的反馈加工阶段，不同社会距离下的损失厌恶估计值

注：*表示p＜0.05，**表示p＜0.01，***表示p＜0.001。图片来源：作者绘制。

为了检验决策阶段对损失厌恶的影响，我们将决策的价值评估阶段（第十二章中的正式实验）与本章所研究的决策的反馈加工阶段进行对比。选取第十二章中行为数据的原因在于：该研究中的正式实验与本实验一样，均采用了包含多种决策类型的风险决策任务，二者在参数设计及收益计算上完全一致，唯一的区别在于是否向被试呈现决策后的反馈结果。因此两项研究具有较高的可比性。我们选取了两项研究中基于个人水平的损失厌恶估计值，通过重复度量的混合设计方差分析检验了被试内因素（社会距离：自己vs朋友vs陌生人）和被试间因素（决策阶段：价值评估vs反馈加工）对损失厌恶影响的主效应和交互效应。方差分析结果确认了社会距离因素主效应［F（2，108）＝11.33，p＜0.001，η2＝0.173］，进一步的配对样本t检验结果显示，损失厌恶程度在为社会距离最近的自己（t＝4.27，p＜0.001）和社会距离较近的朋友（t＝-3.89，p＜0.001）决策时显著高于为社会距离最远的陌生人决策时。决策阶段因素的主效应也得到了证实［F（1，54）＝3.06，p＝0.086，η2＝0.054，边际显著］，这说明损失厌恶估计值在反馈加工阶段（M＝1.13）中比在价值评估阶段（M＝1.27）更小（图14.4）。

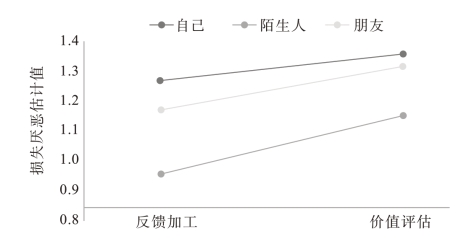
图14.4　不同决策阶段不同社会距离下的损失厌恶估计值