（一）Hopfield网络及其算法简介

1982年，美国物理学家J.J Hopfield教授提出了一种可模拟人脑联想记忆功能的新的人工神经元模型，后来被称为Hopfield网络。Hopfield网络是一种单层全反馈网络，研究的是一种复杂的动力学系统，该系统通过神经元的状态变迁，最终稳定于某一稳定状态，获得联想记忆或神经计算的结果。本书采用二值型Hopfield网络进行城市环境竞争力的后综合评价，验证半监督学习评价结果的合理性。

离散Hopfield神经网络是一种单层、输出为二值神经网络，由13个神经元组成的离散Hopfield神经网络的结构如图8-3所示。这里出于稳定性考虑，选用ωij＝0的无自反馈的Hopfield神经网络。每个神经元t时刻的输入值为xi（t），二值化后的输出值为yi（t），则t时刻神经元的输入值为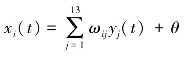：，其中θ为神经元的阈值即外部输入，ωij为神经元i与神经元j之间的连接权值，则t＋1时刻的输出为：yi（t＋1）＝f（xi（t））。

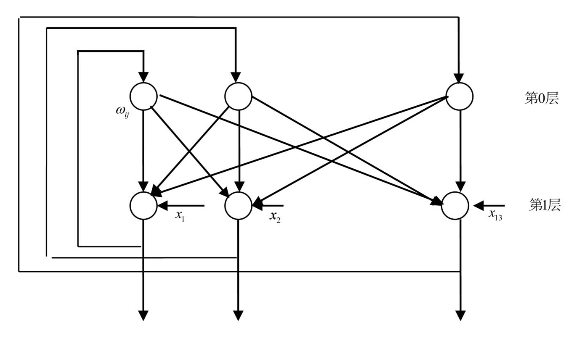
图8-3　离散Hopfield网络结构图

在图8-3中，第0层仅仅作为网络的输入，它不是实际神经元，所以无计算功能；第1层是神经元，故而执行对输入信息与权系数的乘积求累加和，并经非线性函数f处理后产生输出信息。f是一个简单的阈值函数，如果神经元的输出信息大于阈值θ，神经元输出取值为1；小于阈值θ，神经元输出取值为－1。

对于二值神经元，它的计算公式如式（8-30）所示：

式中，xj为外部输入，并且有

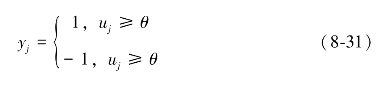
一个离散型神经网络的网络状态是输出神经元信息的集合，对于一个输出层是n个神经元的网络，其t时刻的状态为一个n维向量:

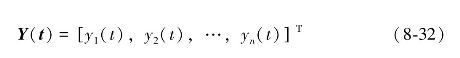
因为可以取值为1或－1，故n维向量Y（t）有2n种状态，即网络有2n种状态。考虑离散型Hopfield神经网络的一般节点状态，用yi（t）表示第j个神经元，即节点j在时刻t的状态，则节点的下一个时刻t＋1的状态可以如式（8-33）、式（8-34）求得：

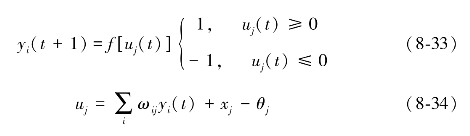
如果ωij在i＝j时等于0，说明一个神经元的输出并不会反馈到其输入，此时离散型Hopfield神经网络称为无自反馈的网络。如果ωij在i＝j时不等于0，说明一个神经元的输出会反馈到其输入端，这时离散型Hopfield神经网络称为自反馈的网络。

（二）Hopfield网络工作方式

Hopfield网络的工作方式主要有两种形式。

（1）串行（异步）工作方式。在任一时刻t，只有某一神经元i（随机的或确定的选择）依据公式变化，而其他神经元的状态不变。

（2）并行（同步）工作方式。在任一时刻t，部分神经元或全部神经元的状态同时改变。

下面以串行（异步）工作方式为例说明Hopfield网络的运行步骤：

第一步，对网络进行初始化。

第二步，从网络中随机选取一个神经元i。

第三步，计算该神经元i的输入ui（t）。

第四步，计算该神经元i的输出vi（t＋1），此时网络中其他神经元输出保持不变。

第五步，判断网络是否达到稳定状态，若达到稳定状态或满足给定条件则结束；否则转到步骤2继续运行。

这里网络的稳定状态定义为，若网络从某一个时刻以后状态不再发生变化，则称网络处于稳定状态。

（三）网络稳定性简介

Coben和Grossberg在1983年给出了关于Hopfield网络稳定的充分条件，他们在文献中指出：如果Hopfield网络的权系数矩阵W是一个对称矩阵，并且对角线元素为0，则这个网络是稳定的。即在权系数矩阵W中，如果：

则Hopfield网络是稳定的，进一步推导过程见相关文献。^[11]

（四）离散Hopfield神经网络学习规则

本书的学习规模主要是正交化法，总体算法过程如下：

第一步，输入N个输入模式及参数τ，h。

第二步，计算。

第三步，对A做奇异值分解A＝USVT，并计算A的秩K＝rank（A）。

第四步，分别由计算。

第五步，计算Wτ＝Tp－τ×Tm，bt＝tN－Wτ×tN。(www.daowen.com)

第六步，计算W＝exp（h×Wτ）。

第七步，计算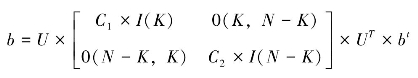，其C1＝exp（h）－1，，具体的公式推导和样本收敛证明可以参考相关文献。^[12]

（五）城市生活环境综合评价结果

影响城市竞争力排名的因素有很多，本书通过第二章筛选出了8个影响因素作为评价指标。根据本书的数据量和综合指数，将城市竞争力分为四个等级：很好（Ⅰ）、好（Ⅱ）、较好（Ⅲ）、一般（Ⅳ）。本书结合离散Hopfield神经网络的联想记忆能力，建立离散Hopfield城市生活竞争力评价模型。

其核心思想是：首先建立典型分类等级所对应的Hopfield神经网络平衡点并进行学习，学习结果即为各分类等级所对应的评价指标并被存储记忆。当待分类指标进入时，Hophield神经网络就会即根据其所存储的平衡点对分类指标进行分类。

1.城市生活环境竞争力理想的等级评价指标

本书所用的13个城市的生活环境竞争力排名等级与8个评价指标之间的关系如表8-20所示。

表8-20　13个城市竞争力等级及对应的评价指标

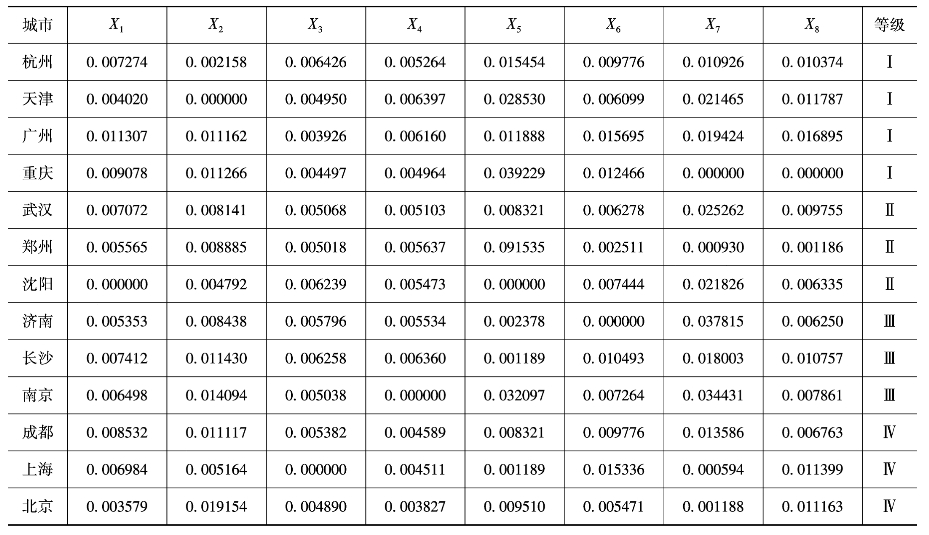
将各个等级样本对应的各评价的平均值作为各个等级的理想评价指标，即为Hopfield神经网络的平衡点，如表8-21所示。

表8-21　四个等级理想评价指标

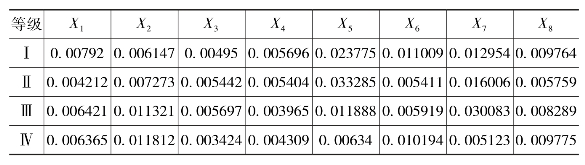
2.理想的等级评价指标编码

由于离散型Hopfield神经网络神经元的状态只有1和－1两种情况，编码规则为：当大于或等于某个等级的指标值时，对应的神经元状态设为“1”；否则为“－1”。理想的4个等级评价编码如图8-4所示，其中●表示神经元状态为“1”，即大于或等于对应等级的理想评价指标值，反之则用○表示。

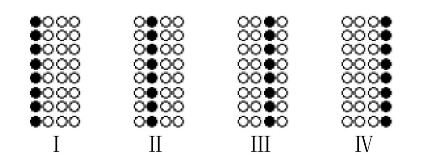
图8-4　等级评价图

3.待分类的等级评价指标编码实现

13个待分类的城市竞争力评价指标根据上述规则设计好理想的4个等级评价指标及编码后，即可利用MATLAB自带的神经网络工具箱函数创建离散型Hopfield神经网络，如图8-5所示。将仿真结果与真实的等级进行比较，可以对该模型进行合理的评价。

图8-5　待分类的13个城市竞争力等级评价指标编码仿真结果

由图8-5可以看出：

（1）第一层是默认层，即按照理想指标进行分类。当某一城市属于具体某一个级别时，它所在的那一列便呈现出实点（黑色）状。

（2）第二层和第三层分别为实际层和训练层。实际层为第四章最终计算的得分分类结果，而训练层是经过Hopfield训练后的分类结果。本章以实际层为标准与训练层进行对比，可以发现，经过训练后的Hopfield分类实点与实际层的分类实点分布基本趋同，即二者分类效果较为一致；

（3）经过比较可以得出Hopfield网络和T-S模糊系统综合评价得到的分类结果都比较接近，说明T-S模糊系统综合评价的结果合理。由于城市生活环境T-S模糊系统综合评价中用到了贝叶斯正则化的神经网络赋权结果，因此此方法也验证了本书引入的新的赋权方法的合理性。

【注释】

[1]张目，李伟，贺颖.基于模糊Borda法的战略性新兴产业企业信用评价[J].科技管理研究，2014，34（5）：65-68.

[2]孙博文，刘艳春.基于模糊Borda组合评价法的电力行业上市公司经营绩效评价[J].管理科学，2013，43（10）：1-8.

[3]李刚，程砚秋，董霖哲，王文君.基尼系数客观赋权方法研究[J].管理评论，2014，26（1）：12-22.

[4]白雪梅，赵松山.多种综合评价方法的优劣判断研究[J].统计研究，2007（7）：45-48.

[5]俞立平，潘云涛，武夷山.基于结果一致度的学术期刊组合评价研究[J].中国科技期刊研究，2011（1）：59-64.

[6]陈衍泰，陈国宏，李美娟.综合评价方法分类及研究进展[J].管理科学学报，2004，7（2）：69-79.

[7][OL].[2020-09-25].http：//baike.baidu.com/view/2585512.htm.

[8]俞立平，姜春林.科技评价指标与评价方法辨识度的测度研究[J].图书情报工作，2013（3）：38-41.

[9]俞立平，潘云涛，武夷山.比较不同评价方法评价结果的两个新指标——以《泰晤士报高等教育副刊》大学排名为例[J].南京师大学报（自然科学版），2008（3）：135-140.

[10][OL].[2020-11-15].http：//baike.baidu.com/item.

[11]韩振东.人工神经网络的数学模型建立及成矿预测的BP网络实现[D].吉林大学，2004；张良均，曹晶，蒋世均.神经网络实用教程[M].北京：机械工业出版社，2008（2）：156-184.

[12]张良均，曹晶，蒋世忠.神经网络实用教程[M].北京：机械工业出版社，2008：156-184.