2009年Zhou和Ang提出了Shannon-Spearman测度方法，用以计算各种评价方法的信息损失量（SSM值）的大小。^[4]利用该方法结合蒙特卡洛方法进行Bootstrap抽样，以信息损失量最小为标准选择最合适的测度方法。其主要思路为：首先，计算各个测度指标的信息损失值（SSM值）；其次，由于SSM值的统计特征（包括标准差和置信区间等）是未知的，因此龚锋和雷欣（2010）认为需要根据蒙特卡洛方法及Bootstrap抽样技术，估计SSM值的标准差和置信区间，以计算各个综合评价指标的信息损失量的精度及可靠性，从而比较分析各个综合评价指标的优劣。^[5]基于Shannon-Spearman测度的优良性选择方法的具体步骤如下。

（一）Shannon-Spearman测度值（SSM值）的计算公式

其中，m＝N×T；N是被评价对象的个数，在本书中有30个省市（N＝30）；T是评价的年数（本书T＝10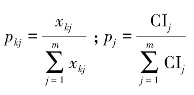）；；rsk是xk与参照向量r0的斯皮尔曼秩相关系数；rs是测度指标CI与参照向量r0的斯皮尔曼秩相关系数，参照向量为r0＝（m，m－1，…，3，2，1）T。

分别将CI设定为加权平均法、加权乘积法、加权重置理想法、逼近理想点排序法等综合评价指标，即可以计算得出这些综合评价指标的信息损失值。

（二）用Bootstrap抽样方法获得SSM值的置信区间

在进行Bootstrap抽样时，需要考虑资源利用指标的样本的面板数据结构。根据Kato、Galvao和Montes-Rojas（2010）的Monte Carlo模拟结果，在个体重复Bootstrap抽样、时期重复Bootstrap抽样、个体-时期重复Bootstrap抽样三种抽样方法中，当个体N和时期T的个数适中时，个体重复Bootstrap抽样的效果最好。在本书资源利用指数的测度研究中采用个体重复Bootstrap抽样法获得SSM值的Bootstrap样本。令CIi.为T×1维的综合评价指标向量，其元素为第i省T年的资源利用综合评价数值；Xi.是T×K维（K是资源利用指标体系中的指标个数，本书K＝13）的原始指标矩阵，其元素是第i省T年K个原始指标值。将CIi.和Xi.组合成T×（K＋1）维的矩阵（CIi.，Xi.），i＝1，2，…，N。具体的Bootstrap抽样过程如下：(www.daowen.com)

第一，对矩阵（CIi.，Xi.）以1/N的概率进行有放回的重复抽样，获得Bootstrap样本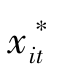（，），i＝1，2，…，N；t＝1，2，…，T。

第二，按个体顺序将N个省份T年的Bootstrap样本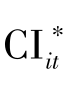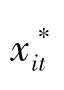（，）综合在一起，形成综合的Bootstrap样本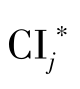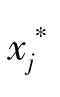（，），其中，j＝1，2，…，N×T。计算汇总Bootstrap样本的信息损失值SSM*：

其中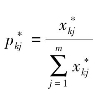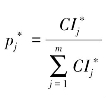，；；m＝N×T；k＝1，2，…，K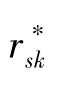；是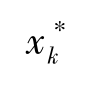与参照向量r0的Spearman秩相关系数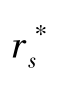；是CI*与参照向量r0的Spearman秩相关系数。

第三，重复上述过程1000次，获得1000个SSM*值，构成SSM的Bootstrap样本。根据Bootstrap样本频数分布的分位数，即可得到其置信水平为95%的置信区间。

根据上述计算结果，信息损失量SSM值最小，且Bootstrap样本的标准误最小的综合评价方法，其评价结果更具有鲁棒性，因此也就是最优的综合评价方法。