人们开始对原来的状态参数提出某一概率分布,后来通过调查又获得许多信息,只要原来信息不是错误的,则应该用后来的补充信息修正原来的认识,并用补充的情报改进原来的概率分布。
将依据过去的信息或经验由决策者估计的概率称为主观概率;
未收到新信息时,根据已有信息和经验,估计出的概率分布称为先验概率;
用随机试验确定出的概率称为客观概率;
收到新信息,修正后的概率分布称为后验概率。
在事件B 已经发生的条件下,事件A 发生的概率,称为事件A 在给定B 下的条件概率:
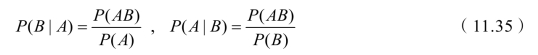
下面给出贝叶斯公式:
若A1,A2,…构成一个完备事件,P(Ai)>0,则对任何概率不为零的事件B,有
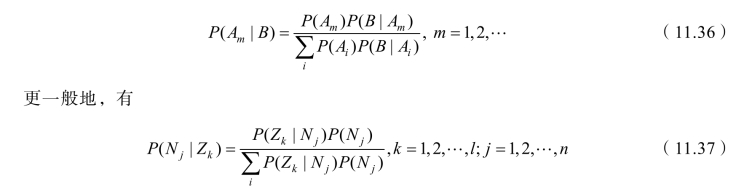
公式(11.37)为后验概率。
例如,根据以往的经验,产品需求量的概率如表11-14 所示。
表11-14

产品进入市场进行两个月试销后,需求量的样本信息(比例)如表11-15 所示。
表11-15

例11-7 盒子里有100 枚均匀的硬币,其中,有60 枚是正常的,有40 枚两面都是国徽。从盒子中任取一枚让你猜是哪一类硬币,猜中得5 元,猜不中不得钱。你猜是哪一类?
表11-16

获利的期望值:
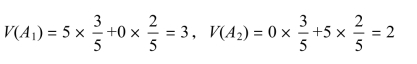
正确的决策是:应该选择猜正常。
如果现在抛掷3 次,3 次都出现国徽,你又如何猜?该硬币是正常的概率为多少?是双国徽的概率为多少?
设H 为3 次出现反面这一随机事件,B1为硬币正常这一事件,B2为硬币双国徽这一事件,则
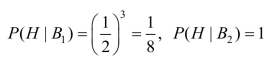
3 次都出现双国徽的概率为:
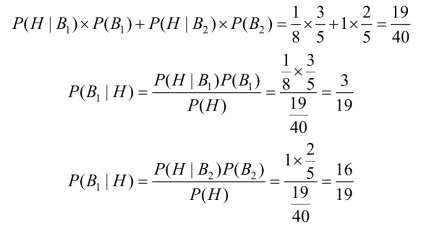
用后验概率代替原来的概率,决策矩阵如表11-17 所示。
表11-17

获利的期望值
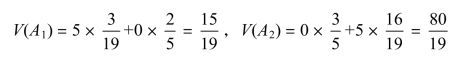
正确的决策是:应该选择猜双国徽。
根据过去经验可知,在自然状态为Nj条件下调查结果为Zk的条件概率为:
![]()
再利用贝叶斯公式和全概率公式,求在结果为ZK的条件下自然状态为Nj的条件概率:
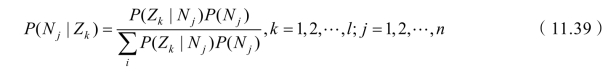
在后验分析中,用 P(Nj| Zk)代替先验分析中的P(Nj),利用期望值准则计算出Ek:
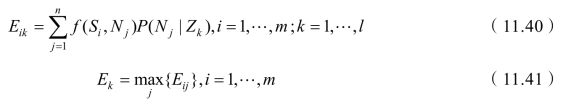
再根据全概率公式,可知结果为Zk的概率为

因此,后验分析的效益期望值为

当状态只有两个时,后验概率及期望收益可用快捷公式计算。记先验概率向量为P,条件概率矩阵为A,后验概率矩阵为B,收益矩阵为V,则(www.daowen.com)
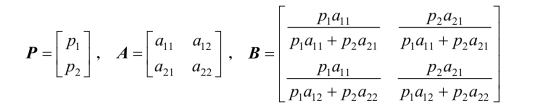
则先验收益期望值向量为
![]()
后验收益期望值矩阵为
![]()
例 11-8 某厂领导需对一台机器的换代问题做决策,其中有三种方案可供选择:A1为买另一台新机器;A2为对老机器进行改建;A3是维护加强.输入不同质量的原料,三种方案的收益如表11-18 所示。约有30%的原料是质量好的,可以花600 元对原料的质量进行测试,这种测试的可靠性如表11-19 所示,求最优方案。
表11-18

表11-19

解 (1)若不做测试,各方案的先验收益分别为:
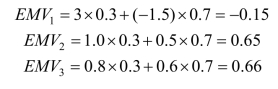
则![]() 万元,应选方案3,维护老机器。
万元,应选方案3,维护老机器。
(2)计算后验概率。
已知![]() 则联合概率为:
则联合概率为:
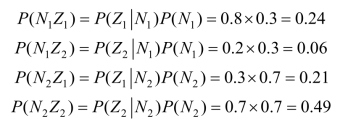
边际概率为
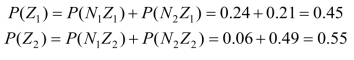
代入式(10.2),从而可得后验概率:

即当测试结果为原料的质量好,则购买新机器;若测试结果为原料的质量差,则维护老机器。
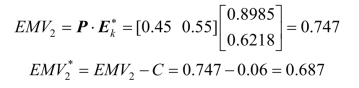
决策为:应花600 元进行测试,测试后若质量好,购入新机器生产;若质量差,维护老机器生产。
例11-9 石油开发决策问题。
表11-20
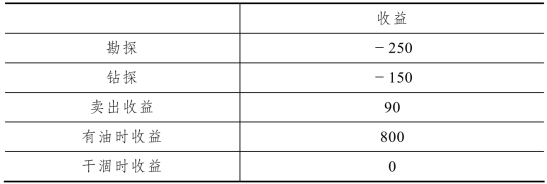
表11-21

表11-22

表11-23
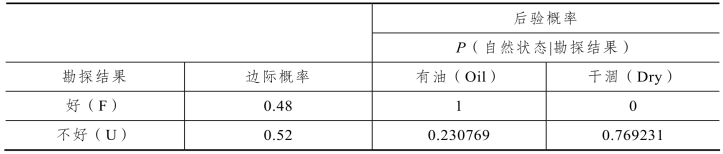
勘探好的概率:
![]()
勘探不好的概率:
![]()
勘探不好时有油的概率
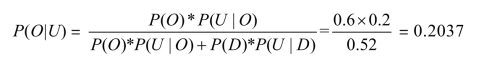
勘探不好时干涸的概率
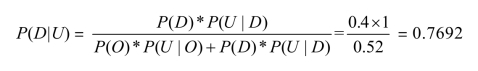
勘探好时干涸的概率
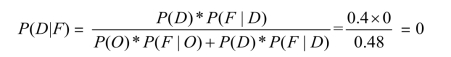
勘探好时有油的概率
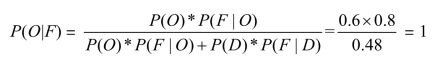
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





