在模型三中，没有考虑补货时间，而事实上，大部分产品的补货是需要一定时间的。因此，模型四进一步放松了模型三的假设，假设订货不是一次性完成的，而是需要考虑补货时间。补货是连续均匀的，补货速度P 是常数，同时假设P＞R。模型四的存储示意图如图9-6 所示。

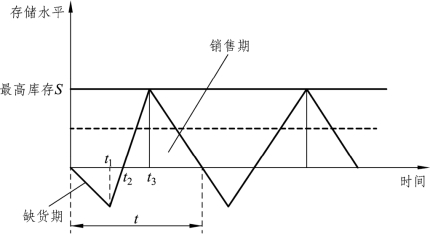
图9-6　模型四的存储示意图

在模型四中，[0，t1]时间内，存储为零，缺货量达到最大值B；t1时刻开始订货，[t1，t2]时间内除满足需求外，同时以速度（P-R）补足[0，t1]时间内的缺货；[t2，t3]时间内以速度R 满足需求后，剩余的产品进入存储且存储量以（P-R）速度增加，在 t3时刻达到最大存储量S 后停止订货。[t3，t]时间内存储量以速度R 减少直到存储为零，进入下一个周期。

在该模型中，各项费用构成情况如下：

订货费用：[0，t]周期内的平均订货费用为

存储费用：[t2，t]时间内的最大存储量为S，则在[0，t]周期内的平均存储量为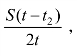平均存储费用为(www.daowen.com)

缺货费用：[0，t2]时间内的最大缺货量为B，则[0，t]周期内的平均缺货量为平均缺货费用为

因此，[0，t]周期内的平均总费用为

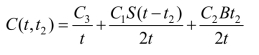
由于有S=（P-R）（t3-t2）和S=R（t-t3），则有（P-R）（t3-t2）=R（t-t3），从而得又由于B=Rt1和B=（P-R）（t2-t1），从而可得因此平均总费用可整理为

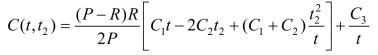
对t 和 t2求偏导，并令其分别等于零，则有