8.1　某工地为了研究发放工具应设置几个窗口，对于请领和发放工具分别做了调查记录：

（1）以10 分钟为一段，记录了100 段时间内每段到来请领工具的工人数，如表8-6 所示。

表8-6

（2）记录了1000 次发放工具（服务）所用时间（秒），如表8-7 所示，试求：

表8-7

续表

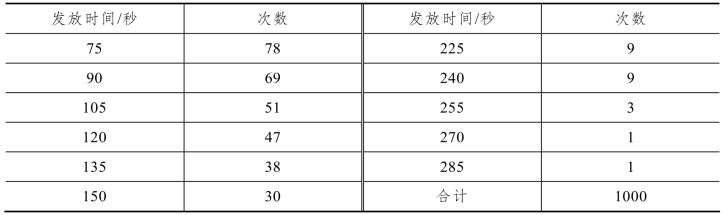
① 平均到达率和平均服务率（单位：分）

② 利用统计学的方法证明：若假设到来的人数服从参数λ=1.6的泊松分布，服务时间服从参数μ=0.9的负指数分布，这是可以接受的。

（3）这时只设一位服务员是不行的，为什么？试分别就服务员数C＝2，3，4 各情况计算等待时间Wq，注意用表8-8。

表8-8　多服务台Wq·μ的数值表

（4）请领工具的工人等待的费用损失为每小时6 元，发放工具的服务员空闲费用损失为每小时3 元，每天按8 小时计算，问设几位服务员才能使总费用损失为最小？

8.2　某修理店只有一名修理工人，来修理的顾客达到次数服从泊松分布，平均每小时4人，修理时间服从负指数分布，平均需要6 分钟，求：

（1）修理店空闲时间概率；

（2）修理店内有3 名顾客的概率；

（3）修理店内至少有1 名顾客的概率；

（4）修理店内顾客的平均数；

（5）修理店内顾客的平均逗留时间；

（6）修理店内等待服务的顾客平均数；

（7）修理店内平均等待修理（服务）时间；

（8）顾客必须在修理店内消耗15 分钟以上的概率。

8.3　某单人理发店的顾客到达为泊松流，平均到达间隔为20 分钟，理发时间服从负指数分布，平均时间为15 分钟。求：

（1）顾客来理发不必等待的概率；

（2）理发店内顾客的平均数；

（3）顾客在理发店内的平均逗留时间；

（4）若顾客在理发店内的平均逗留时间超过1.25 小时，则店主将考虑增加设备及理发员，问平均到达率提高多少时，店主才做这样的考虑？(www.daowen.com)

8.4　称顾客为等待所费时间与服务时间之比为顾客损失率，用R 表示。试证明：对于M/M/1 模型，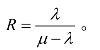

8.5　设 ns表示系统中的顾客数，nq表示队列中等候的顾客数，在单服务台系统中，我们有

试说它们的期望值

根据此关系式给ρ 以直观解释。

8.6　某工厂为职工设立了昼夜24 小时都能看病的医疗室（按单服务台处理）。病人到达的平均间隔时间为15 分钟，平均看病时间为12 分钟，且服从负指数分布，因工人看病每小时给工厂造成损失为30 元。

（1）试求工厂每天损失的期望值；

（2）问平均服务率提高多少，方可使上述损失减少一半？

8.7　对于M/M/1/∞/∞模型，在先到先服务情况下，试证明：顾客排队等待时间分布的概率密度是

并根据上式求等待时间的期望值Wq。

8.8　对于M/M/1/N/∞模型，试证明：

并对上式给予直观的解释。

8.9　某新工厂正在决定分配给一个特别的工作中心多少存贮空间。工作以平均每小时三个的泊松分布被送到工作中心，工作中心每次只能执行一个工作，完成该工作所需要的时间遵从每小时0.25 个的指数分布。若工作到达时工作中心已满，则工作需转放到一个不方便的地方。如果每个工作在工作中心存放时需要一平方米的空间，工厂希望工作中心内的空间能够保证90%的时间里容纳下全部到达的工作，需要分配多少空间给工作中心？（提示：几何数列的和

8.10　在习题8.2中，如修理店内已有3 名顾客，那么后来的顾客即不再排队，其他条件不变。试求：

（1）修理店内空闲的概率；

（2）各运行指标 Ls，Lq，Ws，Wq。

8.11　在习题8.2中，若顾客平均到达率增加到每小时12 人，仍为泊松流，服务时间不变，这时增加了一名工人。

（1）根据 λ /μ的值说明增加工人的原因；

（2）增加工人后求修理店的空闲概率；修理店内有两个或更多顾客（即工人繁忙）的概率；

（3）求 Ls，Lq，Ws，Wq。

8.12　机场有两条跑道，一条专供起飞用，一条专供降落用。已知要求起飞和降落的飞机都分别按平均每小时25 架次的泊松流到达，每架飞机起飞或降落占用跑道的时间都服从平均2 分钟的负指数分布。又设起飞和降落时彼此无关。

（1）试求一架飞机起飞或降落为等待使用跑道所需的平均时间；

（2）若机场拟调整使用跑道办法，每条跑道都可作起飞或降落用。但为了安全，每架飞机占用跑道时间延长为平均2.16 分钟的负指数分布，这时要求起飞和要求降落的飞机将混合成一个参数为50 架次/小时的泊松流到达流。试计算这种情形下的平均等待时间。

（3）以上两种方法哪个更好呢？

8.13　在习题8.2中，如服务时间服从正态分布，数学期望值仍是6 分钟，方差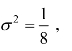求修理店内顾客数的期望值。