6.1　证明如下序列不可能是某个简单图的次的序列：

（1）7,6,5,4,3,2；

（2）6,6,5,4,3,2,1；

（3）6,5,5,4,3,2,1.

6.2　已知九个人 v1，v2，…，v9中 v1和两个人握过手，v2，v3都和四个人握过手，v4，v5，v6，v7都和五个人握过手，v8，v9都和六个人握过手，证明这九个人中一定可以找出三人互握过手。

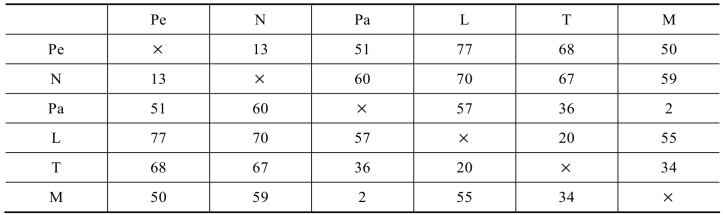
6.3　已知世界六大城市：（Pe），（N），（Pa），（L），（T），（M），试在由表6-6 所示交通网络的数据中确定最小树。

表6-6(www.daowen.com)

6.4　设G=（v，E）是一个简单图，令（称 δ（G）为G的最小次）。

（1）证明：若 δ（G）≥2，则G 必有圈；

（2）若 δ（G）≥2，则G中必包含至少 δ（G）+1 条边的圈。

6.5　设G 是一个连通图，不含奇点，证明：G中不含割边。

6.6　试证明下述论断正确与否：可行流f的流量为零，即 v（f）=0，当且仅当f 是零流。

6.7　已知有六台机床 x1，x2，…，x6，六个零件 y1，y2，…，y6，其中机床x1可加工零件y1；机床x2可加工零件y2，y3；机床x3可加工零件y1，y2，y3；机床x4可加工零件y2；机床x5可加工零件y2，y3，y4；机床x6可加工零件y2，y5，y6。现要求制订一个加工方案，使一台机床只加工一个零件，一个零件只在一台机床上加工，要求尽可能多地安排零件的加工，试把这个问题化为求网络最大流的问题，求出能满足上述条件的加工方案。