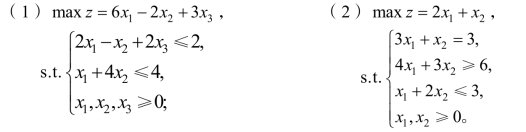
2.2 已知某线性规划问题，用单纯形法计算时得到的中间某两步的计算情况如表2-19所示，试将表中空白数字填上。
表2-19
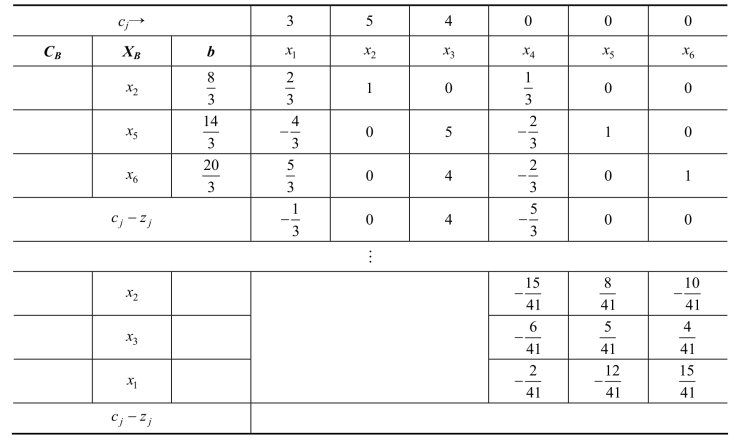
2.3 写出下列线性规划问题的对偶问题。
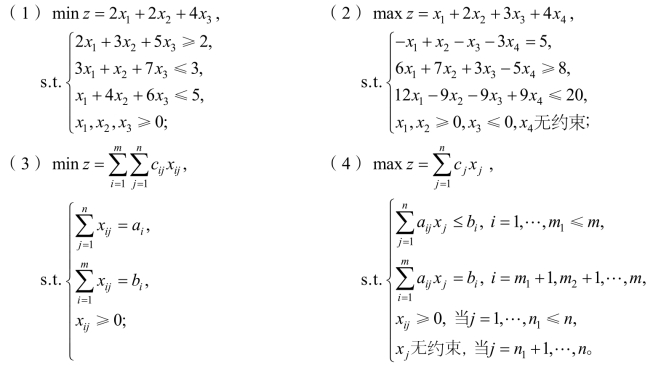
2.4 判断下列说法是否正确，为什么？
（1）如线性规划的原问题存在可行解，则其对偶问题也一定存在可行解；
（2）如线性规划的对偶问题无可行解，则原问题也一定无可行解；
（3）如果线性规划的原问题和对偶问题都具有可行解，则该线性规划问题一定具有有限最优解。
2.5 设线性规划问题1 是：
2.6 已知线性规划问题max z=CX，AX=B，X ≥0，分别说明发生下列情况时，其对偶问题的解的变化：
（1）问题的第k 个约束条件乘上常数 λ（λ≠0）；
（2）将第k 个约束条件乘上常数 λ（λ≠0）后加到第r 个约束条件上；
（3）目标函数max z=λCX（λ≠0）；
（4）模型中X=（x1，x2，…，xn）T用
代换。
2.7 已知线性规划问题：
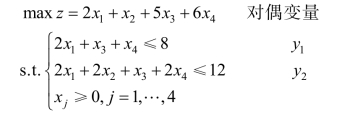(www.daowen.com)
其对偶问题的最优解为
试应用对偶问题的性质，求原问题的最优解。
2.8 试用对偶单纯形法求解下列线性规划问题。
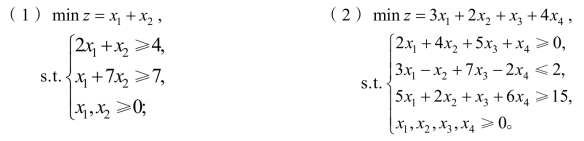
2.9 设有线性规划问题：
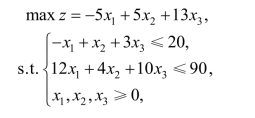
先用单纯形法求出最优解，然后分析在下列各种条件下，最优解分别有什么变化？
（1）约束条件①的右端常数由20 变为30；
（2）约束条件②的右端常数由90 变为70；
（3）目标函数中 x3的系数由13 变为8；
（4）约束条件中 x1的系数列向量由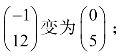
（5）增加一个约束条件③：2x1+3x2+5x3≤50；
（6）将原约束条件②改变为：10x1+5x2+10x3≤100。
2.10 已知某工厂计划生产Ⅰ，Ⅱ，Ⅲ三种产品，各产品需要在A，B，C 设备上加工，有关数据如表2-20 所示。
表2-20
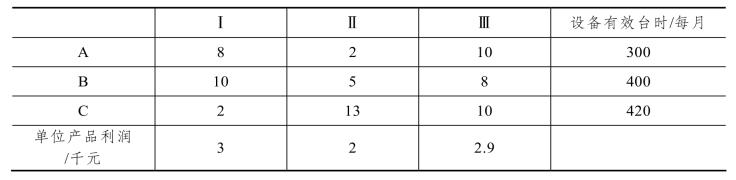
试回答：（1）如何充分发挥设备能力，使其生产盈利最大？
（2）若为了增加产量，可借用其他工厂的设备B，每月可借用60 台时，租金为1.8 万元，问借用B 设备是否合算？
（3）若另有两种新产品Ⅳ，Ⅴ，其中新产品Ⅳ需用设备A，12 台时，设备B，5 台时，设备C，10 台时，单位产品盈利2.1 千元；新产品Ⅴ需用设备A，4 台时，设备B，4 台时，设备C，12 台时，单位产品盈利1.87 千元。如A，B，C的设备台时不增加，分别回答投产这两种新产品，在经济上是否合算？
（4）对产品工艺重新进行设计，改进结构。改进后生产每件产品Ⅰ，需用设备A，9 台时，设备B，12 台时，设备C，4 台时，单位产品盈利4.5 千元，问这对原计划有何影响？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
