11.1 某厂考虑生产甲、乙两种产品,根据过去市场需求统计如表11-31 所示。
表11-31 甲、乙产品市场需求数据

用最大可能法进行决策。
11.2 对第11.1 题用期望值法进行决策,并进行灵敏度分析,求出转折概率。
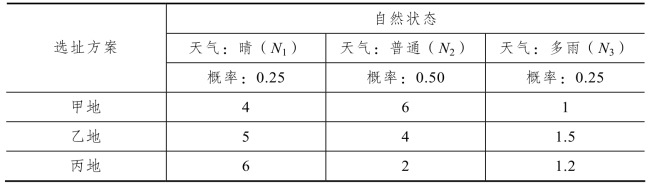
11.3 某公司为了扩大市场,要举行一个展销会,会址打算选择甲、乙、丙三地。获利情况除了与会址有关系外,还与天气有关。天气可区分为晴、普通、多雨三种(分别以N1,N2,N3表示)。通过天气预报,估计三种天气情况可能发生的概率为0.25,0.50,0.25。其收益情况如表11-32 所示,用期望值准则进行决策。
表11-32 收益情况表 单位:万元
11.4 对第11.3 题用矩阵法进行决策。
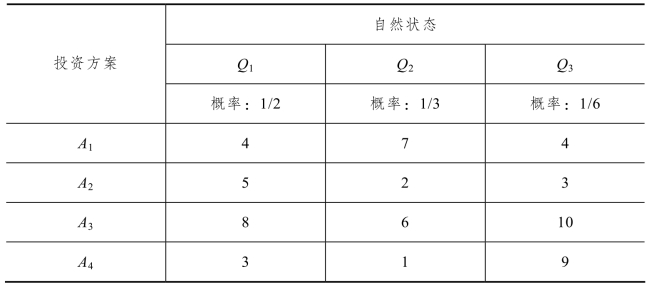
11.5 现要建立一个企业,有四个投资方案,三种自然状态,投资数量如表11-33 所示。
表11-33 各投资方案数量表 单位:百万元
用矩阵法进行决策。
11.6 某公司正考虑是建大厂还是建小厂来生产一种新产品,该产品的市场寿命W 为10年,建大厂的投资费用为280 万,建小厂的投资为140 万。10 年内销售状况的离散分布的状态如下:
高需求量的可能性为0.5;
中等需求量的可能性为0.3;
低需求量的可能性为0.2。
公司进行了成本-产量-利润分析,在工厂规模和市场容量的组合下,它们的条件收益如下:
(1)大工厂,需求高,每年获利100 万元。
(2)大工厂,需求中等,每年获利60 万元。
(3)大工厂,低需求,由于开工不足,引起亏损20 万元。
(4)小工厂,高需求,每年获利25 万元(供不应求引起销售损失较大)。
(5)小工厂,中需求,每年获利45 万元(销售损失引起的费用较低)。
(6)小工厂,低需求,每年获利55 万元(因工厂规模与市场容量配合得好)。(www.daowen.com)
用决策树方法进行决策。
11.7 对第11.5 题用决策树法进行决策。
11.8 对第11.6 题用矩阵法决策。
11.9 对第11.3 题用决策树法进行决策。
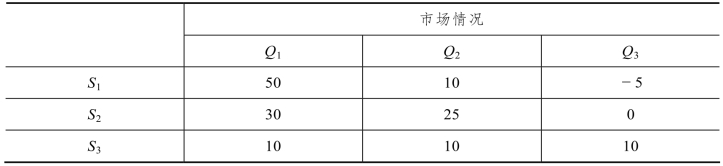
11.10 某厂有一种新产品,其推销策略有S1,S2,S3三种方案可供选择,但各方案所需的资金、时间都不同,加上市场情况的差别,因而获利和亏损情况不同。而市场情况也有三种:Q1(需求量大),Q2(需求量一般),Q3(需求量低)。市场情况的概率并不知道,其损益矩阵,如表11-34 所示,用乐观法进行决策。
表11-34 损益矩阵 单位:万元
11.11 对第11.10 题用悲观准则进行决策
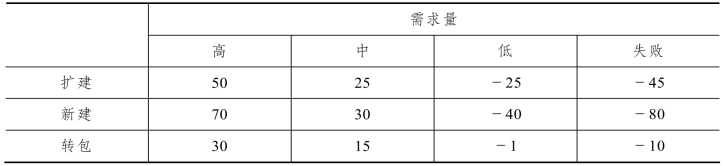
11.12 某企业面临三种方案可以选择,五年内的损益表如表11-35 所示,用乐观系数法( α1=0.3,α2=0.7)决策,然后加以比较:
表11-35 损益表 单位:万元
11.13 对11.12 题用等可能准则进行决策,并与上题比较结果。
11.14 在开采油井时,出现不定情况,用后悔值准则决定是否开采。损益矩阵如表11-36所示。
表11-36 损益矩阵表

11.15 某企业要投产一种新产品,投资方案有三个:S1,S2,S3,不同经济形势下的利润如表11-37 所示。用乐观系数准则( α1=0.6,α2=0.4)进行决策。
表11-37 利润表 单位:万元
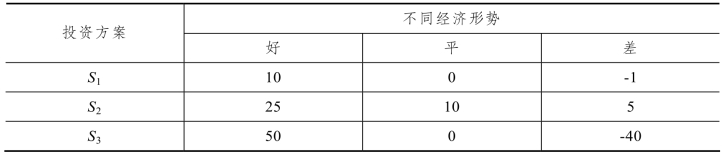
11.16 对1.15 用等可能准则进行决策。
11.17 建厂投资有三个行动方案可以选择,并有三种自然状态,其损失如表11-38 所示。用乐观准则进行决策。
表11-38 损益表
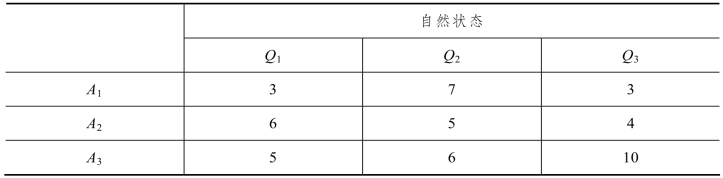
11.18 对11.17 题用悲观准则进行决策。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








