1.何谓散布图？

为了了解两种数据间的关系，而将这两种数据以有序成对的方式，在直角坐标上点绘成图。两种数据可为：

（1）要因与特性：比如，焊锡温度与焊点不良、反应温度与收量。

（2）要因与要因：比如，反应温度与反应液浓度、反应温度与压力。

（3）特性与特性：比如，身高与体重。

2.散布图的绘制方法

步骤一：明确目的，决定调查的对象。

步骤二：收集数据——50～100组“成对数据”（最少30组）。

步骤三：分别找出两种数据之最大值及最小值。

步骤四：绘纵轴、横轴并作适当刻度（刻度大小应考虑最大值与最小值之差），通常横轴表示要因，纵轴表示特性。

步骤五：将成对数据于图上打点。

步骤六：记入必要事项：

（1）标题。

（2）数据之测定日期、绘制日期、绘制者。

（3）样本数。

（4）产品名称、制程名称。

3.散布图的看法

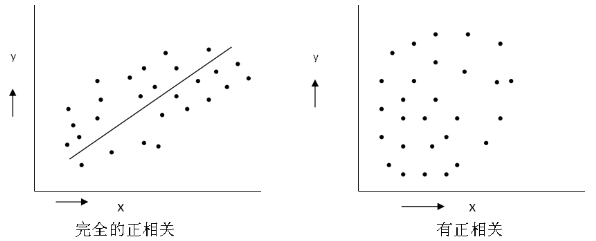
（1）正相关：x增大时，y也随着增大，参照图6-15。

(www.daowen.com)

图6-15　正相关散布图

（2）非显著性正相关：x增大时，y也随之增大，但幅度不显著；此时宜再考虑其他可能有影响的要因，参照图6-16。

图6-16　非显著性正相关散布图

（3）负相关，x增大时，y反而减少，参照图6-17。

图6-17　负相关散布图

（4）非显著性负相关：x增大时，y反而减少，但幅度不显著。此时宜再考虑其他可能有影响的原因，参照图6-18。

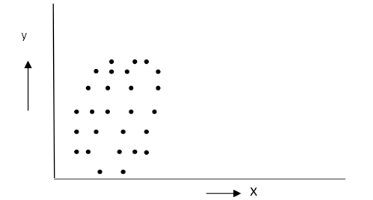
图6-18　非显著性负相关散布图

（5）无相关：①x与y之间看不出有何相关关系；②x增大时，y并不改变，参照图6-19。

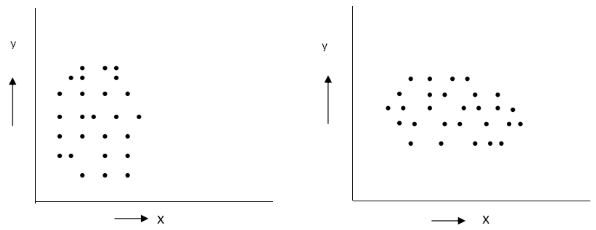
图6-19　无相关散布图

（6）曲线相关：x增大时，y也随之增大，但达到某一值后，则当x增大时，y却减少，参照图6-20。

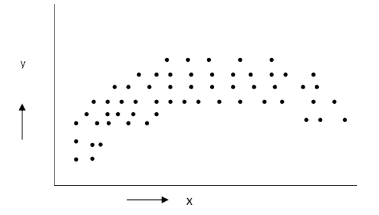
图6-20　曲线相关散布图

4.散布图的应用

（1）了解相关关系，并掌握应加管理改善之处。

（2）条件设定之参考。