本章将胜任力水平作为因变量，以农产品个体网商胜任力模型的素质因素作为自变量，运用回归分析工具作多元线性回归分析，得出结论后运用最小二乘法进行模型评估。之后从中把t值达到0.05的显著标准筛选后进入回归 方程。

4.4.1　线性回归前提假设检验

要展开接下来的研究，首先要确保回归模型的基本假设符合线性回归的基本要求。具体验证过程如下：

首先，通过绘制散点图来判断因变量和自变量之间是否满足线性关系的要求。根据之后的研究可以判断因变量胜任力水平与农产品个体网商胜任力模型的素质因素之间存在线性关系，符合回归分析的要求。

图8-4　因变量与自变量线性关系散点图

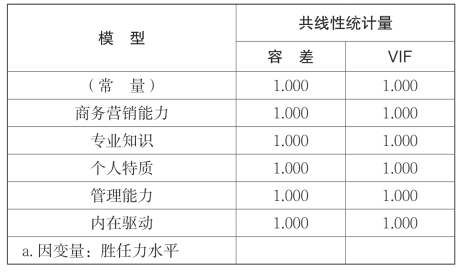
其次，采用了DW检验方法检验因变量的独立性。残差各项之间要相互独立，DW值就越接近2。数据的统计分析结果DW＝2.008，残差间趋向于无相关，因变量具有独立性。而自变量的独立性，可以采用多重线性检验判断。多重线性就是检验因变量之间的彼此关系，一般通过容忍度和方差膨胀因子两个指标来判断。容忍度处于0—1之间，容忍度越接近0，说明自变量之间存在共线性关系；方差膨胀因子（VFI）是容忍度的倒数，当VFI小于10的时候，说明自变量不存在多重共线性。根据表8-9可知，自变量之间不存在多重共线性。

最后，检验比较两组数据的方差，检验他们的精密度是否有显著性差异。如图8-5可知，多数观测量散落在0点水平线的两侧，预测值与残差之间没有明显的相关，回归方程满足方差齐性假设。

表8-9　农产品个体网商胜任力模型素质因素共线性检验结果a(www.daowen.com)

4.4.2　回归模型分析

经过上文对多元线性回归前提假设的检验，得出因变量农产品个体网商胜任力水平与自变量之间可以展开多元线性回归分析，具体的分析结果见 表8-10：

表8-10　农产品个体网商胜任模型素质因素与胜任力水平之间的回归分析结果

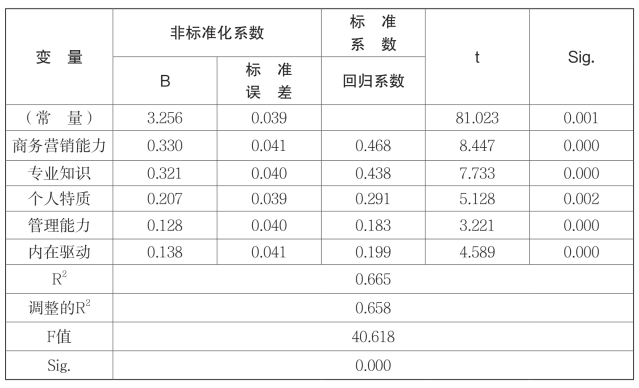
如表8-10表示，R2＝0.665，修正的R2＝0.658，说明方程的拟合度较优， F＝40.618，Sig＝0.000，低于显著性水平的最低标准0.05，说明回归方程显著性水平较高，并且经过方差显著性检验后，可得出专业知识、商务营销能力、管理能力、个人特质、内在驱动这5个素质指标因素的回归系数P值都小于0.05水平，显著性水平较高。因此，该回归方程模型具有现实意义。

通过回归分析结果不难发现，5个胜任力素质因素都有显著性的标准化回归系数，且5个胜任力素质因素都列入回归方程，其中，商务营销能力的标准化回归系数最高，说明其与其他能力相比对农产品个体网商胜任力水平的影响最为显著。