如何生动高校数学课堂

武汉东湖学院基础课部　周　雪

如何生动高校数学课堂？本文从三个方面来回答这个问题：（1）让数学建模思想融入高校数学课堂；（2）让数学文化融入数学课堂；（3）让数学实验融入数学课堂。

一、引言

提到数学，公众对数学的认识状况令人担忧，这已经成为一个国际性的问题。面对数学抽象的符号、严密的逻辑、高深的理论，一般人只好望而却步。他们不理解数学，害怕数学，有的可能知道数学有用，但无法领会其用处何在；有的干脆认为数学毫无用处。提到大学数学，大学生们更多的是在应付期末考试，或者为了考研需要而应试做题。所以对于大学的数学课堂，学生到底在学什么？老师到底又在教什么？学生通过课堂怎么学习数学？老师通过课堂怎么教学？为什么我们高校的数学课堂不能丰富、生动起来呢？我认为，大学的数学课堂其实可以做到比高中的数学课堂要“丰富”、“生动”。

二、让数学建模思想融入高校数学课堂

在课堂上要最大化的激发学生对数学的学习兴趣,培养学以致用的意识和能力,关键还要激发他们对数学重要性和应用性的再认识。除了应将基本概念、定义、定理、方法讲清、讲透之外，我们还要将数学建模思想融入到数学课堂，例如在教学过程中适当的引入与课堂知识相关的简单“数学模型案例”，这是比较行之有效的办法。数学模型本身就是用数学方法解决实际问题的手段和桥梁，直接面向现实，走近生活，很容易使学生领悟到数学工具在解决实际问题中的强大威力，使学生有直接、切身的认同感。

1.数学模型案例教学

〖案例1〗在讲授闭区间上连续函数的零点存在定理时，除了列举一些常规的零点定理应用例子之后，特给出如下问题：妹妹小英过生日，妈妈给做了一块边界形状任意的蛋糕（见图1）。哥哥小明见了也想吃，小英指着蛋糕上的一点对哥哥说，你能过这点切一刀，使切下来的两块蛋糕面积相等，我便把其中的一块送给你。小明苦想了半天，你知道他用的是什么办法？

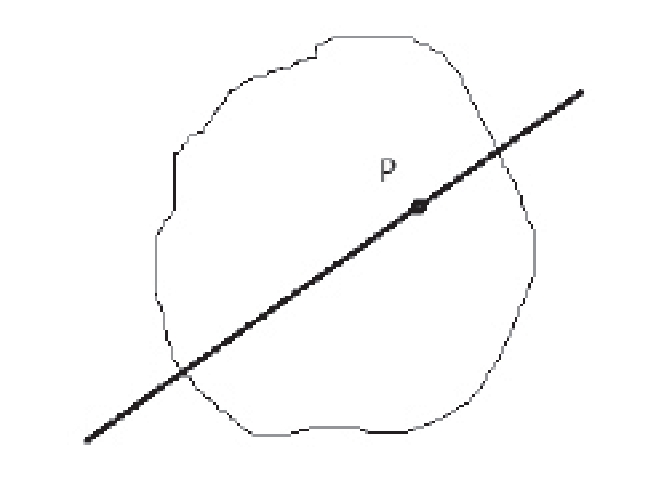
图1

证明：(1)过P点任意作一直线l，将曲线所围成图形分为两部分，其面积分别记为S₁、S₂（见图2）。若S₁=S₂（此种情况很难办到），则l即为所求；若S₁≠S₂，则不妨设S₁＞S₂(此时l与x轴正向的夹角记为α₀,)下面对此情况证明。

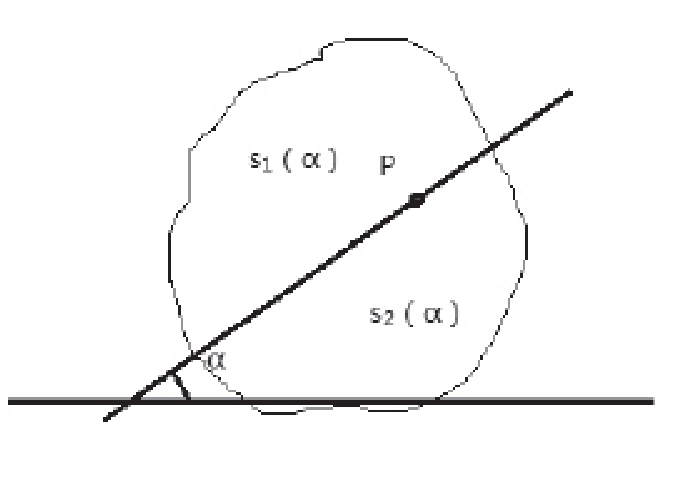
图2

(2)以P点为旋转中心,将l按逆时针方向旋转,面积S₁、S₂就连续地依赖于角α变化,记为S₁(α)、S₂(α),并设f(α)=S₁(α)－S₂(α)。

(3)函数f(α)在[α₀，α₀+π]上连续，且在端点异号：

f(α₀)=S₁(α₀)－S₂(α₀)＞0

f(α₀+π)=S₁(α₀+π)－S₂(α₀+π)=S₂(α₀)－S₁(α₀)＜0

根据零点定理,必存在一点ξ∈(α₀，α₀+π),使f(ξ)=0，即使S₁(ξ)－S₂(ξ)=0,或S₁(ξ)=S₂(ξ)。过P作直线,使之与x轴正向的夹角成ξ,该直线即为所求。

〖案例2〗在讲授微分方程的解法时，可以例举如下例子：在凌晨1时警察发现一具尸体，测得尸体温度是29℃，当时的环境温度是21℃，一小时后尸体温度下降到27℃，人的正常体温是37℃。请帮助警察估计死者死亡的时间。

问题分析：根据牛顿冷却定律，将温度为T的物体放入温度为T₀的介质中，则该物体的温度T的变化速率正比于该物体与周围介质温度差T－T₀。由于速度刻画的物体在某时刻的变换率涉及导数概念，因此反映在数学模型上必然可以运用微分方程来建模。

模型建立：现就一般情形考虑，有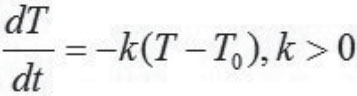为比例常数（由物体和介质的性质决定，而负号则表示温度是下降的）。设该名死者已经死亡t₁小时，于是根据题意得到如下的微分方程模型：

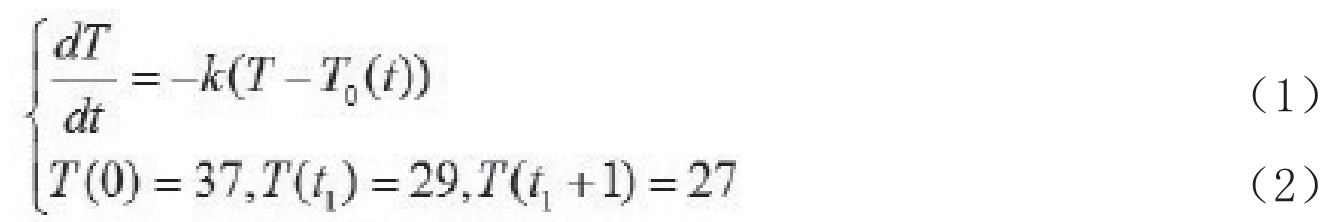
模型求解：利用分离变量方法解得方程（1）式的通解为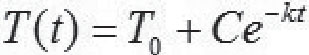，代入（2）式及T₀=21，得到：

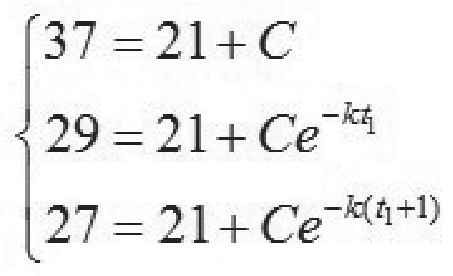(www.daowen.com)

解上述方程得。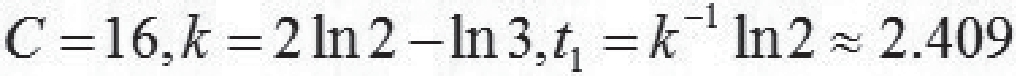

于是可知该死者死于2.049小时前，即前一天夜晚10时35分左右。该模型的解为：

模型分析与应用：上述模型的建立实际上是假设环境的温度恒定为T₀=21℃不变，在此前提下，上述模型可以很好的推算出死者的死亡时间。但是如果死者的死亡时间较长，显然环境的温度应该是有所变化的，从而上述模型可以改进为非自治的情形：

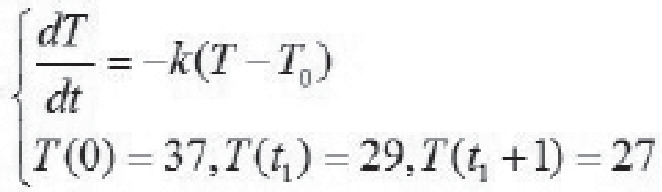
其中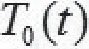是描述环境温度随时间变化的函数。此方程是一阶线性的，其通解为：

在已知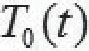的情况下，类似的方法可以求得t₁的值。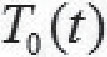可以是经验函数，也可以通过环境温度的变化数据拟合得到。

2.数学建模竞赛走入课堂

提到数学考试，大家能想到的就是不要挂科。提到数学竞赛，大家能想到的就是畏惧。所以我们可以尝试改变考试形式，例如把期中考试计入平时成绩，而期中考试可以以数学建模竞赛的形式考核，选做一道简单的数模题。数学建模竞赛是区别于其他比赛及考试的一种开放性的竞赛，三人组成一队，可以交流、找资料、查找信息等。当然，期末考试的形式还是不变，对基本知识的考查还是有必要的。

三、让数学文化融入高校数学课堂

在数学教育过程中，应通过数学文化的渗透，将方方面面都结合起来。正如爱因斯坦所认为的那样，热爱才是最好的老师，它永远超过责任心。探索奥秘的感觉是美好而深刻的，如果没有了这种感觉，一个人就会丧失在心灵的神圣颤栗中如痴如醉的能力，他的生活将是无趣的。数学文化使得各种人文因素在教学过程中优化组合，滋润渗透，洋溢着情趣，充满着智慧，使学生在浓浓的人文氛围中潜移默化地形成了一定的人文修养，也增加了学习数学的兴趣。

1.数学文化名人故事讲学

数学这门古老的科学，它的诞生和发展的道路是崎岖不平的，其间凝聚着无数数学家的艰苦追求和不懈探索。可以说，数学的发展史就是数学家们不断战胜挫折的奋斗史，没有挫折就没有奋斗，就没有数学的发展。在数学史的学习中，无数数学家的成功事例及其艰苦探索的过程，能够鼓励学生大胆探索，也可以锻炼他们勇于吃苦的精神。

例如：欧拉，生于瑞士，是18世纪数学界的中心人物，可与数学史上的三大数学家阿基米德、牛顿和高斯并列。欧拉18岁开始发表论文，31岁积劳成疾，右眼失明，在接下来25年中，欧拉为柏林和彼得堡科学院递交百篇科学论文，64岁双目失明，此后17年中，欧拉是在全盲中度过。虽然经历了失明、火灾和丧偶的多重打击，但他凭着顽强的毅力、超人的才智、渊博的知识，又发表了多部专著和近400篇论文。欧拉的数学论著是惊人的多产，足迹遍及至今数学的所有部门，他在微积分、微分方程、曲线曲面的解析几何、微分几何、数论级数、变分法上都有卓越的贡献，他首创了现在一直通用的一些数学符号，如f(x)、sin、cos、tan、∑等。

数学文化里有很多名人故事，如牛顿、莱布尼兹、伯努利家族、、柯西、高斯等。

2.数学发展史进入课堂

数学的每一次发展，都是科学价值的体现。当所谓的数学危机到来时，似乎给人们带来了困惑，但为解决数学危机所做的努力以及数学价值观的应用却使科学的观念深入人心，使数学科学价值成为人类认识数学世界的重要思想武器，也使数学科学理论日益完善。通过数学文化的传承，使受教育者初步了解了数学与人类社会发展之间的相互作用，体会到数学的科学价值与人文价值，开阔了视野，努力寻求数学进步的历史轨迹，激发了对于数学创新原动力的认识。

从数学发展史上看，每一次重大的发展，总是与人类的思想观念相互作用、相互影响而紧密联系在一起的，这就使数学理论不可避免地体现出某种自然观、社会观、科学精神和人文精神。

由此可见，数学文化不仅能影响人的自然观，也能影响人的社会观。数学作为人类精神文明的成果，不仅闪烁着人类智慧的光芒，而且还体现了人类为真理而奋斗的精神。数学文化的传承，可以使所有享受数学的人认识数学发展的历史、了解先辈数学家的奋斗经历与科学品质，从而内化到受教育者的身心之中，使之受到教育。

四、让数学实验融入高校数学课堂

除了在数学教学过程中融入数学建模思想和数学文化，给学生以一种直观的感受之外，更重要的是要让学生能自主思考，自行运用建模的方法解决实际问题，逐步培养用数学进行分析、推理和计算的能力，培养和发展学生熟练运用计算机和各种数学软件的能力，使数学在他们手中真正变成一个有力的工具。

数学课堂可以适当融入多媒体教学，当然，多媒体使用越多，教学质量不一定越好。所以不是所有的课都适合使用多媒体，但是个别教学内容可以搭配多媒体教学。在多媒体教学课堂上，可以适当的加入一些数学软件的基础教学。现在有些学生对Word编辑里面的数学公式编辑器（Mathtype）的一些基本使用完全不知道，这不仅是数学能力缺失的表现，更是一个时代能力的缺失。再例如在教高数时可以引进Mathmatica基础教学，让大家了解积分求导等是可以简单运行计算的；线性代数也可以引进Matlab教学，计算相关的矩阵运算。还可以使用一些画图工具，如Matlab、几何画板等，让学生发挥自己的聪明才智，享受学以致用的快乐。

综上所述，高校数学课堂是可以生动起来的，这个问题需要更多的教育者来进行深入研究。