在埃尔热的漫画书《太阳神的囚徒》中，年轻的比利时记者丁丁误闯太阳神庙，被印加部落的人囚禁起来。印加人要将丁丁和他的朋友阿道克船长和卡尔库鲁斯教授烧死在木桩上。放在木柴上的放大镜聚焦太阳光从而引燃木桩。虽然他们允许丁丁选择执刑时间，但他能否借助这点来拯救他自己和朋友们的生命呢？

丁丁做了一系列的数学运算后，发现几天之后该地区将出现一次日食，于是，他便把行刑时间设在日食发生的时间段内。（事实上，做这些数学运算的另有其人，丁丁只是在一份剪报上看到了这个消息。）就在日食即将发生之前，丁丁喊道：“太阳神不会听到你们的祷告！伟大的太阳，若不愿我辈赴死，请赐降福信！”说话间，正如数学运算预测的那样，太阳消失不见了，部落里的人们大惊失色，立即释放了丁丁和他的朋友们。

数学是一门发现模式的科学，而这正是它能够预知未来的原因所在。在古代，观测星空的天文学家们很快意识到，月亮、太阳及行星的运行轨迹是循环往复的。许多文明都利用这些天体模式来划分时间。由于太阳和月亮在天空划过时遵循一种奇妙的切分节奏，出现了各种不同的历法。不过，这些历法有一个共同点，即数学在其中都发挥了重要的作用，人们通过数学记录下月亮和太阳的运转周期，并以此来标记时间。其中，数字19在确定每一年复活节等节日的具体日期时发挥了重要的作用，这一点十分有趣。

所有这些历法中的基本单位都是一天24个小时。24小时并非地球自转一周的时间，后者稍短一点，为23小时56分4秒。若我们把这个稍短一点的时间设定为一天的时间，那么，我们的时钟将和自转的地球逐渐脱节，因为多出来的3分56秒将日积月累，直到有一天，当时钟指向正午的时候，我们却在经历午夜。因此，为计时的需要，我们将一天（或更准确地说，一个太阳日）确定为太阳回到天空中同一位置所需的时间，同一位置的参照点是我们在地球表面的某一点上看到的。在一次自转之后，地球将沿其轨道移动1/365个循环，因此，它需要继续自转1/365的幅度，即1/365天（约为3分钟56秒）的时间，才能使太阳回到天空中同一个位置上。

再精确一点的话，地球需要365.2422个这样的太阳日才能围绕太阳旋转一周。格里高利历法（即多数国家所使用的历法）正是建立在这一周期的近似值之上的。多出的0.2422接近四分之一，因此，每过4年就在格里高利日历中增加1天，从而大体上与地球围绕太阳轨道旋转的步调保持了协调一致。不过，由于0.2422并非真正的四分之一，因此，在历法中还要做一些微调：每过100年，我们会替换掉1个闰年，而每过400年，则要停止替换，保留这样一个闰年。

伊斯兰历法采用的的则是月球周期。其历法中的基本单位为太阴月，12个太阴月构成1个太阴年。太阴月以麦加上空的新月初现为始，约有29.53天。这样算下来，1个太阴年要比1个太阳年短了11天。365除以11约等于33，因此，要花33年的时间，斋月才能在太阳年中走过一轮，这也正是为何斋月逐渐溜走的原因了，正如格里高利历法推算的那样。

犹太人和中国人的历法则是将两者搭配起来使用，同时借鉴了地球围绕太阳旋转的周期和月亮围绕地球旋转的周期。他们通过每过大约3年时间添加1个闰月的方式来构建历法，其中的运算关键则要仰赖这个神奇数字19。19个太阳年（=19×365.2422天）和235个太阴月（=235×29.53天）几乎完全吻合。在中国历法中，每19年的轮回中有7个闰年，以保持阳历和阴历的协调一致。

数字19在丁丁的运算中也发挥着十分重要的作用，因为日食月食的出现顺序也是以19年为周期而循环往复的。上文中《太阳神的囚徒》的这一情节基于的其实是一桩著名的历史事件：1503年，当探险家克里斯多弗·哥伦布和他的船员在牙买加身陷困境时，便是利用月食（并非日食）让整个团队摆脱了危难。起初，本地人对哥伦布的船队十分友善，后来却充满敌意，并拒绝向他们提供食物补给。面对饥饿的部下，哥伦布想出了一个巧妙的计划。他翻阅历书（海员航海使用的一本书，其中包含对于潮汐、太阴周及恒星位置的预测）发现将在1504年2月29日这一天出现月食。哥伦布在月食降临前3天召集当地民众，并恐吓他们：如果他们不提供补给，他就让月亮消失不见。

下次的日食/月食何时出现？

如果知道一次日食/月食的时间，你便可通过数学公式计算出另外一次出现日食/月食的时间。这些运算要依赖两个重要的数字。(www.daowen.com)

第1个数字就是太阴月的组成天数29.5306 (S )。这是月球围绕地球一周并返回同一位置（相对于太阳）所需的平均时间。它是两轮新月之间的时间间隔。

第2个数字则是交点月的组成天数27.2122 (D )。月球围绕地球旋转的轨道面和地球围绕太阳旋转的轨道面之间有一个细微的倾斜角度。两条轨道相交于两个位置，我们称之为月球轨道交点，如图5-1所示。交点月即月球旋转一圈，并再次回到第一个交点所用的平均时间。

只要能找到任何一对整数A 和B，能使A×S 和B×D 所得的值十分接近，那么自你看到最后一次日食/月食A×S≈B×D 天之后便会出现另一次日食/月食。依此类推，再经过A×S≈B×D 天后，还会再出现一次日食/月食。这种日食/月食序列还会持续一段时间，但是，由于以上等式并不完全相等，因此，这些日食/月食的效果会越来越不明显，直到太阳、月亮和地球不再连成一条直线为止。此时，这一特定的日食/月食周期便终结了。

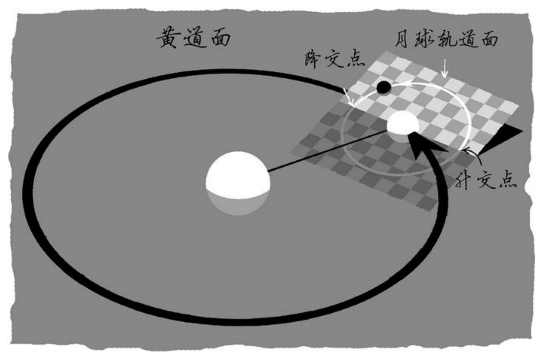
图 5-1　月球轨道与地球轨道相交于两点，分别称为升交点和降交点

举例来看：当A=223个太阴月，B=242个交点月时，A×S 和B×D的值非常接近，因此，每个日食/月食之后的每223×29.5306≈242×27.2122天便会出现另外一次可辨识的日食/月食。这段时间大约为6585又1/3天，即18年11天8小时。8个小时的时差表明，我们将在地球的其他位置上看到之后的2次日食/月食。但是，第3次仍会出现在同一地点，因此，每经过3个18年11天8小时，即大约19 756个完整日后，在同一地点将重现同样的日食/月食。

例如，2010年12月21日在北美观测到的月全食便是1992年12月9日在欧洲所观测到的月食的重现。而上一次在美国观测到月全食则是在1956年11月18日。介于这些日期之中也曾出现过其他月食，但它们都属于其他月食周期。数学能够帮助我们计算出每个周期中的下一次月食/日食出现的时间。

补给并没有送来——这些本地人不相信哥伦布拥有令月亮消失的力量。但是，在2月29日当晚，当月亮从地平线升起时，人们看到月亮已经缺了一角，就像被咬过一样。据哥伦布的儿子费迪南德描述，随着月亮逐渐从夜空消失，这些人大为惊恐，“嚎哭声、悲泣声，响彻云霄，人们从四面八方蜂拥至舰队停泊之地，运来满满的补给品，哀求这位海军上将代表他们向他的上帝讲和”。通过精确的计算，哥伦布准确把握着月亮重现的时间，并有意在月亮回归正常之时表现出对本地人的宽恕。或许这个故事的真实性有待考量，或许是西班牙人为了将聪明的欧洲征服者和本地无知的原住民进行对比而有意编撰出这个故事。不过，故事的核心仍表现出了数学的强大力量。

数学预测夜空的能力要依赖于发现这些循环模式。那么，我们要如何预测新事物呢？下面，我们就来介绍一些人类通过数学公式来窥视未来的故事，首先来看对于简单物体（如足球）运动状况的预测。