编码者们永远试图走在密码破解者们的前面。假设质数密码有朝一日会遭到破解也不用担心，数学家们总是不断发现更聪明的传播秘密信息的方式。一种叫做椭圆曲线密码学的新型密码（简称ECC），已经被用于保护飞机的航线安全。本章的百万美元难题便与这些新型密码背后椭圆曲线的数学问题相关。

椭圆曲线有很多种，但它们均满足公式y²=x³+ax +b 。每一条曲线对应着不同的a 和b 的值：比如，当a=0，b=-2时，公式则变为y²=x³-2。

上述的等式便对应着一条特定的曲线，只要找出一系列的坐标点(x ,y )，我们便可以在坐标纸上画出这条曲线，如图4-18所示。先设定一个x 的值，计算出x³-2，再取其平方根作为对应的y 值。比如，如果x =3，那么x³-2=27-2=25。要得到y 的值，我需要取25的平方根，因为y²=x³-2，因此y 的值为±5（因为负负得正，一个数字的平方根永远成双成对）。所以，这条曲线将是一条沿横轴对称的曲线，因为所有正的平方根都有一个对应的负平方根。如此，我们便确定了两个点的坐标(3,5)和(3, -5)。

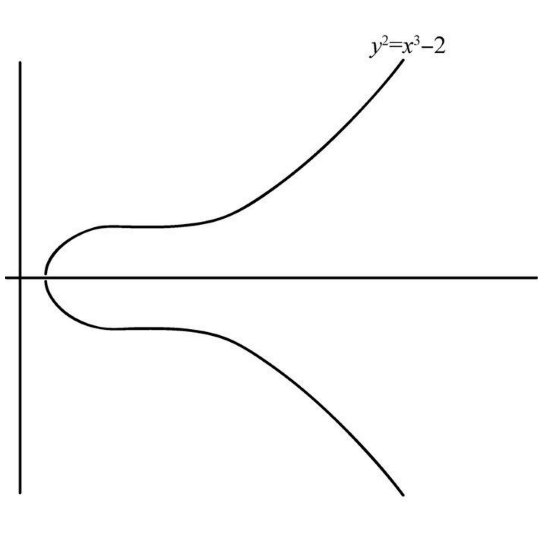
图 4-18　椭圆曲线图

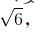这条曲线上的每个点都非常规整，因为其中的x 和y 都是整数。你还能找到其他类似的坐标点吗？我们试试将x 设为2。x³-2=8-2=6，于是y 。在第一个例子中，25的平方根为整数，但是在这个例子中，6的平方根就不是整数。古希腊先贤们早已证实，没有什么分数（更别说整数了）在平方运算后能得到数字6。如果以小数形式表示，那么，它将是一个无穷小数，而且小数点后的数字毫无模式可循。

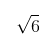=2.449 489 742 783 178…

本章的百万美元难题便和从这条曲线上找到x 、y 同为整数或分数的坐标点这个问题相关联。大多数情况都不满足这种要求，因为选定一个x 值后，得出的y 值很少会是一个整数或哪怕是一个分数，因为大部分数字的平方根都没那么整齐。在这条曲线上找到了(3,5)和(3,-5)这两个点说明我们的运气不错，但是，还有其他这样的点吗？

古希腊人提出了一个绝妙的几何理论，能让我们在锁定一个坐标后继续找出更多的坐标，其中x 和y 都是分数。具体方法是，在第一个点上画一条直线，使其不能穿过曲线，而要以准确的角度切过这条曲线，如图4-19所示。我们将之称为曲线在该点上的切线。通过延长这根切线，它将和曲线相交在另一个点上。令人兴奋的发现就是，这个新交点的坐标也同样皆为分数。

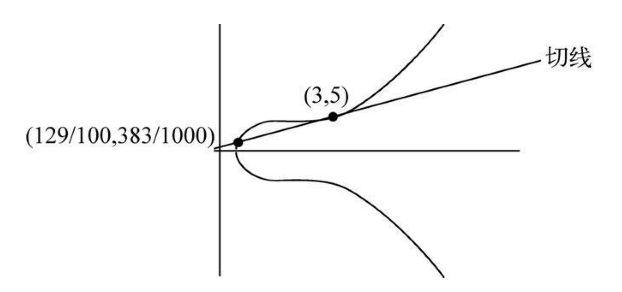
图 4-19　如何在曲线上找到更多坐标都是分数的点

例如，如果我们在椭圆曲线y²=x³-2上的点(x, y)=(3,5)上画一条切线，这条切线将会与曲线上另一个点相交，该点的坐标为(x, y)=(129/ 100,383/1 000)，两个坐标值均为分数。而通过这个新坐标点，我们可以重复上述操作，继续找到下一个x 、y 坐标都为分数的点：

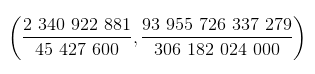
如果没有以上这一几何理论的话，人们很难会发现这样的一个分数值x：

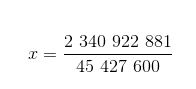(www.daowen.com)

会推导出一个同样也是分数的y 值。

在这个例子中，你可以通过持续重复这一几何思路，寻找到无数个坐标值都为分数的点。对于一条椭圆曲线y²=x³+ax+b 来说，如果有一个点(x₁, y₁)，其中x₁和y₁都是分数，那么坐标组合：

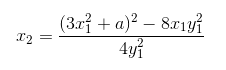
和

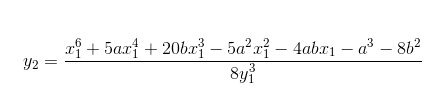
将构成曲线上另一个坐标均为分数的点。

对于这个例子中的曲线y²=x³-2来说，以上两个公式将带来无数个这样的坐标点，但在有些曲线中，我们无法找到无穷多个类似的坐标点。比如以下公式所对应的曲线：

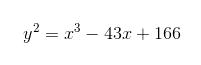
在这条曲线上，只存在有限数量的两坐标均为整数或分数的点：

(x, y )=(0,0),(3,8),(3,-8),(-5,16),(-5,-16),(11,32),(11,-32)

实际上，以上坐标值都是整数。不妨试试通过其中的一组数字，运用上面提及的几何或代数手法，找出更多坐标为分数的点。

本章的百万美元难题称为贝赫和斯维讷通—戴尔猜想，题目是能否找到一种方式，能帮助人们分辨出哪种椭圆曲线中包含无数个x 、y 值均为整数或分数的坐标点。

有人可能会说，谁去在乎这种问题的答案？但事实上，我们每个人都应该在乎，因为椭圆曲线中的这个数学问题如今已应用在手机和智能卡中，以保护我们的隐私，此外还应用在航空控制系统中以确保我们的人身安全。通过这种新型密码，我们的信用卡号码或信息以一种聪明的数学方式被嵌入在曲线上的某个点上。为加密讯息，数学家便通过上文提到的几何方式找出一个新的点，然后再把之前那个点移到这个新位置上。

解开这个几何流程则超出了当今数学的能力范围。但是，如果你能揭开本章的这个百万美元谜团，它或许能帮助你破解掉这些新型密码。果真如此的话，你恐怕也不在乎这区区的一百万美元了，因为你已是这个星球上最强大的黑客了。