一旦密码员发现替换式密码的内在缺陷后，便开始着手设计更巧妙的加密方式，以挫败解码者基于字母频率的破解尝试。

其中一种思路是扩充替换密码的种类。在为整个文本编码时，不再只使用一种替换法则，而是交替地使用两种替换密码。这样一来，比如你要把单词beef进行编码，其中的两个字母e可以替换为两个不同字符，第1个e可以根据一种密码来替换，第2个e则根据另外一种密码来替换。因此，beef有可能会编码为PORK。对信息的安全系数要求越高，你就要加入更多的不同的密码。

当然，在密码学中，密码的安全和可用性之间需要实现一种平衡。最安全的密码称为一次性密码本，它对文本中的每个字符执行一套不同的替换码。这种密文几乎无法破解，因为密文中完全没有任何线索可供你把握。同时，这种密文也会令接收者十分头疼，因为在破解的时候你需要一个字母一个字母地替换回来。

16世纪的法国外交官布莱斯·德·维琼内尔认为，要阻止频率分析法破解密码，只需执行少数几种替换码即可。人们所熟知的维琼内尔密码尽管是一套十分强大的密码法则，但并非坚不可摧，英国数学家查尔斯·巴贝奇最终便找到了一种破解它的方法。巴贝奇被视为计算机时代的始祖，他坚信计算机能执行自动化的计算工作，而他所打造的“差分机”计算机的一个复制品如今依然陈列在伦敦科学博物馆中。正是他在1854年提出的这种系统化处理问题的方法才提供了破解维琼内尔密码的思路。

巴贝奇的方法建立在一种最伟大的数学技巧——模式识别之上。首先，我们要判定出密文中共使用了多少种替换码。因为单词the在任何文本中出现的频率都会很高，从密文中挑出重复出现的三字母的单词便是探明其中运用了多少种替换码的关键切入点。比如，你可能会发现单词AWR总是频繁出现，而在AWR之间，总还会出现一系列的四字单词，这将暗示出密文中使用了4种替换码。

一旦有了这个信息，你就可以把密文拆分为4组。第一组包含第1个字母、第5个字母、第9个字母，依此类推。第二组包含第2个字母、第6个字母、第10个字母等。而在这四组的任何一组中，每个字母所采用的都是同一套替换码，那么，此时你就可以用频率分析法依次对每组字母进行分析，密码最终便可破解。

一旦维琼内尔密码被破解后，人们马上开始寻找安全性更高的编码方式。20世纪20年代，德国研发出了恩尼格玛密码机，许多人就此相信不可破解的终极密码终于创建出来了。

恩尼格玛密码机按照每个字母一套替换码的原则进行密文编写。如果我们把文字编码为序列aaaaaa（或许表示我现在“正承受痛苦”），那么其中的每个字母a都会使用一套不同的密码。恩尼格玛密码机的绝妙之处就在于它把替换码与替换码之间的置换执行得十分高效。信息通过键盘输入，在键盘上方有第2排字母板——“光板”，当用户按下键盘上的一个按键时，上方的字母板中便会有一个字母亮起，表示密文中所显示的字母。但是，键盘并不直接控制上方的光板，两者之间依靠3个转子来建立联系，这些转子包含迷宫式的连接线路，而且它们还能旋转。

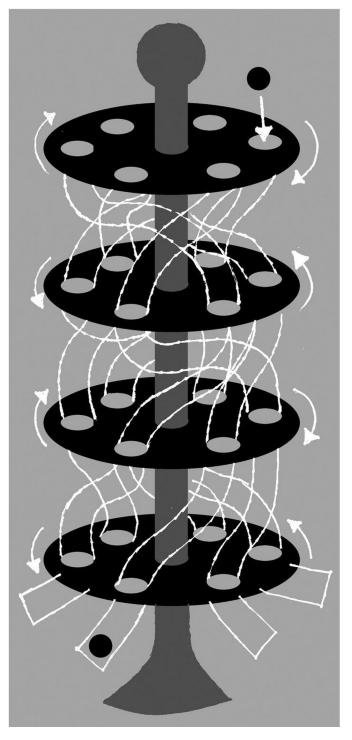
现在，我们来想象一下恩尼格玛密码机的工作方式。设想一个大的圆柱体中有3个滚筒。在圆柱体的顶端，沿着底面边缘钻有26个孔洞，每个孔洞标记1个英文字母。在编码一封信件时，我们将一个小球从对应的字母洞中塞入。小球会落到第1只滚筒中，滚筒上下两端的边缘处各有26个孔洞。上下方孔洞之间由管道连接，但管道并非简单地将上下相对的2个孔洞连接起来，而是混为一团，管道在滚筒中扭曲旋转，因此，顶端掉落下来的小球从滚筒底端的一个完全不同的位置上掉出。中间和偏下的2只滚筒的工作原理也是一样的，只是其中的管道连接方式又完全不同了。当小球从第3只滚筒底端掉出后，它便进入这个巧妙装置的最后一段，接着便会从圆柱底端的26个洞口之中的1个洞口中掉出，同样，这26个孔洞也都标记了字母。

但是，如果该设备的功能仅限于此，那么它只不过是一种更复杂的替换编码方式而已。但是，恩尼格玛密码机的真正妙处正是：每次当一个小球落入圆柱体后，第1只滚筒转动1/26个圆的角度。因此，当第2个小球掉入其中时，第1只滚筒便会将其带向一条完全不同的路径。比如说，字母a可能第一次被编码为字母C，而等到第一只滚筒转动了一次后，第2个掉入a字母洞的小球便会从底部的一个不一样的洞中掉出来。恩尼格玛密码机的工作原理便是如此：当第1个字母被编码完后，第1只转子便会转动一个位置。

转子的旋转方式有点像里程表：一旦第1只转子转完26个位置后，它便回到初始状态，接着第2只转子便开始转动。如此算下来，共有26×26×26种不同的编码方式。此外，设备操作人员还可以调整若干转子的前后排列，进一步地把编码种类扩充6倍（对应3!种不同的转子排列方式）。

恩尼格玛密码机操作员人手一本密码簿，其中记录着每天的工作要开始时，他们将以何种方式排列好这些转子，然后再开始编码工作。接收者也借助于密码簿中的相同设置对文本进行解码。人们在创建恩尼格玛密码机的过程中又加入了更多额外的复杂性，而该设备共提供1.58万亿亿种不同的编码方式。

(www.daowen.com)

图 4-2　恩尼格玛密码机的工作原理：向管道中抛入一个小球来编码一个字母。圆柱体在每次编码后会发生旋转，因此，每次各个字母的编码方式都不同

1931年，法国政府发现德国制定的相关计划时大为惊诧。他们似乎无法从这段截获的信息中了解到转子在每天的编码工作中的设置方式，而它们的设置方式对这些密文的破解十分关键。幸好，法国人和波兰人之间有交换情报的协议，而德国人对波兰领土的虎视眈眈也使波兰的伟大头脑们汇聚了起来，开始致力于破解转子的排列方式。

波兰的数学家们意识到，在每一种转子排列方式中，都隐含一些各自的特征，而这些特征模式则成为破解此类密码的切入点。比如，如果操作员输入字母a，根据转子的设置情况，假设最终编出的字母为D，接着，第一只转子会转动一下，此时，当另一个a被输入后，假设编码出的字母为Z，那么，从某种意义上来说，通过转子的设置情况，字母D和Z之间存在着某种关联性。

我们可以借助于之前的那个奇妙装置来研究一下这件事。重新设置好滚筒，然后依次把小球放入两个相同的字母洞中，便可创建出类似下表中的完整关系列表（表4-3）。

表　4-3

    在本书配套网站中，也有一个指导性的PDF文件供大家下载，有兴趣的读者可以藉此创建出自己的恩尼格玛密码机。

每个字母只出现1次，而且在每排中也只出现1次，因为每1行对应着1套单一的替换密码。

那么，波兰数学家是如何利用这些关系的呢？在任何一天内，德国所有的恩尼格玛密码机操作人员都会根据密码簿的要求，使用同样的转子设置。接下来他们可以选择自己的设置，然后再使用密码簿中的原始设置把密文发送出去。为了安全起见，他们被要求重复自己的选择，重复输入密文内容2次。但是，这种做法非但未能带来安全，反而铸成大错。波兰人从中发现了一条线索，从而了解到这些转子是如何与字母相联的，并以此为切入点，最终探索出每一天的恩尼格玛密码机是如何设置的。

一群数学家住在牛津和剑桥之间布莱切利园的一间乡间别墅里，对波兰数学家们发现的模式展开了研究，并通过他们所打造的一台称为“炸弹”的机器找到了一种自动对这些设置展开搜索的方法。据称，这些数学家所做的工作使二战提前2年结束，因而挽救了无数生命。而他们所创建的机器装置则最终催生了今天我们每个人都无比依赖的电脑。1

1计算机科学之父阿兰· 图灵是此次密码破解工作的核心成员，关于此段往事的回忆，可以参考人民邮电出版社出版的《图灵的秘密：他的生平、思想及论文解读》。——编者注