赛季过半，你所效力的球队沦落到榜单中下游位置，那么，你就想知道，从数学概率上来说，球队是否还有夺冠的可能。有趣的是，回答该问题所要用到的数学思想直接与本章中价值百万美元的难题相关。

要确定上述问题在数学概率上是否可能，首先，你要假定你的球队会一举赢下剩下的所有比赛，从而每场比赛都拿下3分。但是，当你开始在榜单上分配其他积分时，难题就来了。位列榜单前列的球队必须输掉足够多的比赛，以让位给你的球队。但你无法让你前面的所有球队都输球，因为这些球队彼此之间也要打比赛。这就意味着，你必须找到一种方式，根据余下的赛程表来恰当地分配积分，并期望寻找到一种胜负组合，能够让你的球队一举登上宝座。要确定是否存在这样的胜负组合，一定有更聪明的方法吧？

在此，我们要寻找的巧妙方法就是类似欧拉画地图的那种方法，以免于尝试所有可能的比分组合。但遗憾的是，我们现在还不知道这样的技巧是否真的存在。谁能第一个找到这类技巧，或第一个证实该问题的复杂性除了穷尽所有可能外无法得出结果，那么百万美元就归他了。

诡异的是，1981年前，的确存在这么一种有效机制，能够帮助我们确定联赛过半时球队是否还有机会赢得冠军。因为在1981年以前，球队获胜积两分，而如果比赛以平局收场，则参赛双方各得1分。这一规则的数学意义十分重大，它意味着每个赛季的总积分数都是固定的。例如，在英超这种有20支球队参加的联赛中，每支球队1个赛季要打满38场比赛（分别于主客场对阵其他19支球队）。这样总共就有20×38场比赛……但且慢，在这里，每场比赛都被我们算进了2次。例如，阿森纳对阵曼联和曼联对阵阿森纳指的都是同一场比赛。因此，一个赛季中共有10×38场比赛。也就是说，1981年前的积分制度规定，赛季结束后，所有20支球队的积分相加等于2×380=760。这一点便是回答上述问题的有效机制的关键所在。

但是，1981年，一切都在数学意义上改变了。规则变成赢一场比赛获得3分，平局则两队各得1分。我们无法事先预知赛季结束后的总积分。如果每场比赛都以平局收场，总积分将是760分。但如果整个赛季无一平局，那么总积分将是1140分。这中间的差异便是造成英超问题如此难解的原因所在。

如果你对足球不感兴趣，像这样的问题其实还有很多其他版本。其中一个经典案例便是旅行推销员问题。举例来说：假定你是一名推销员，眼下需要拜访11位客户，每位客户都住在不同的城镇，这些城镇之间以道路相连，如图3-17所示。而车里的燃油只够你行驶238英里的路程。

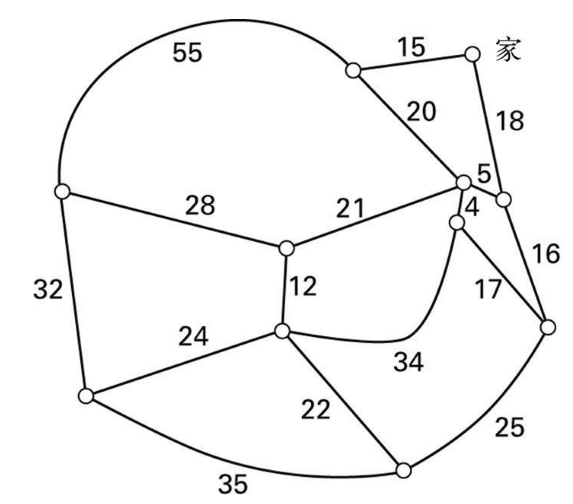
图 3-17　旅行推销员问题。你能否找到一条238英里以内的路径，造访其中的每个点后，再安然返回到出发点呢

连接两个城镇的道路上的数字即是城镇之间的距离。你是否能找到一条成功拜访11位客户并在燃料耗尽前安然返回家中的路径呢？（答案请见本章末尾。）在这个版本的问题中，要想获得百万美元，必须提供一种通行的算法或电脑程序，不管是什么样的地图，只要套进这种算法或程序，便能很快确定出其中的最短路径，而无需用电脑进行一番穷举式的搜索。随着地图中城镇数量的增加，可能的路线数量也会呈指数级增长，从而使穷举式搜索很快变得不切实际。另外，如果能证实此类程序并不存在，你同样也能获得这一百万美元。

数学家们对这类问题的普遍看法是，其中有一种内在的复杂性，因此并不存在任何聪明的解决方法。我将此类问题称为“沙里淘金”问题，本质上来说，这种问题的答案很多，但我们所要寻找的总是某一条特定路径。这类问题还有一个技术称谓，叫做NP完全问题。

这些谜题都具有一个关键特征，那就是一旦你找到了其中的金子，便可以轻易地判定答案是否准确。比如，一旦你在地图上找到一条比238英里短的路径，问题便迎刃而解了。类似地，如果剩余赛程的胜负结果陆续出来，你立刻就能知道，从数学的概率问题上来看，球队是否还存在夺冠的可能。所谓P问题指的就是能够找到快速解答机制的方法。因此，也可以这样描述本章的百万美元问题： NP完全问题是否就是P问题呢？数学家将之表示为NP v P。

另外还有一个与所有这些NP完全问题相关的有趣属性。如果你找到能够解决其中一个问题的高效程序，那么就意味着这个程序也能解决所有其他的这类问题。例如，如果你找到了一个用来确定旅行推销商最短路径的聪明程序，那么，它便可转换为另外一个高效程序，解决球队能否赢得联赛冠军的问题。为说明这一点，我们再来看其他两个看上去十分不同的“沙里淘金”问题，即NP完全问题。

派对策略问题

你想邀请一些朋友参加派对，但其中有些朋友相互之间不和，这就是说，你不能让2个敌人出现在同一房间内。因此，你决定同时举办3个派对，每个派对邀请不同朋友参加。你是否能找到一种分发请帖的方式，以避免互有敌意的人出现在同一个派对呢？

三色地图问题

在第2章中，我们已了解到，不管是什么地图，只要4种标记颜色就足够了。那么，是否存在一种有效的方法，能帮助我们确定不管在任何情况下3种颜色就足够了呢？

三色地图问题的解决方法如何能帮助我们解决派对的策略问题呢？假设你已依次写下朋友的姓名，并在互有敌意的人员之间连一条线，如图3-18所示。

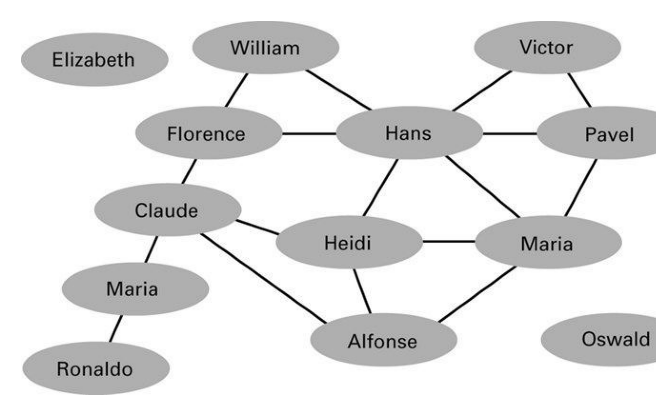
图 3-18　 不能出现在同一派对上的人员之间以线条相连

在确定邀请哪位朋友去哪个派对时，你可以在他们的姓名框内涂上特定颜色，1种颜色代表1个派对。邀请哪位朋友去哪个派对就相当于给上述的姓名框涂颜色，使所有相连的姓名框的颜色都不相同。接下来，让我们把这些朋友的名字替换成其他事物，再来看看情况会发生什么变化（如图3-19所示）。

(www.daowen.com)

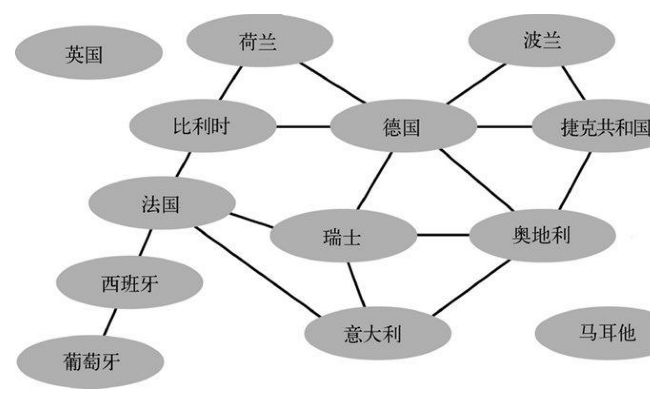
图 3-19　相邻的国家以直线相连

如图3-19所示，互有敌意的朋友都变成了相邻的欧洲国家，而朋友之间的连接线则变成了相邻国家的边境线。因此，选择哪位朋友去哪个派对的问题就变成了选择哪种颜色为欧洲地图上色的问题了。

派对策略问题和三色地图问题只是同一个问题的不同版本，通过这个例子，我们便了解到，只要能找到一种有效的方式解决一个NP完全问题，你最终便会解决掉所有这类问题！下面列出了此类各种不同的问题，你可以试试自己赢得一百万美元的手气如何。

扫雷

这是微软操作系统自带的一款单机游戏。游戏目标是清除1个网格中的全部地雷。如果你点击其中的1个网格，而且没有地雷的话，游戏就会显示出该方格四周的地雷数量；而如果你踩在地雷的位置，便即刻输掉了游戏。百万美元的扫雷挑战则有所不同。比如，图3-20不可能出自一个真正的扫雷游戏，因为这些数字所指示的情况是不可能存在的（图3-20）。方格中的1表示四周未揭开的方格中有1颗地雷，而数字2则表示四周有2颗地雷。

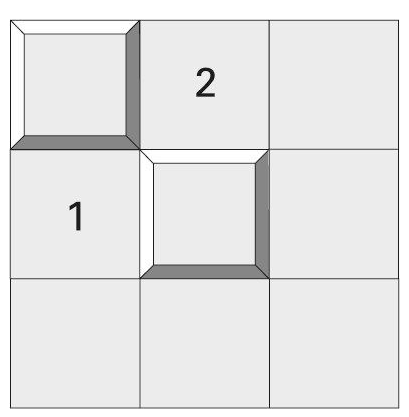
图　3-20

那么图3-21如何呢？它能构成一个真实的扫雷游戏吗？

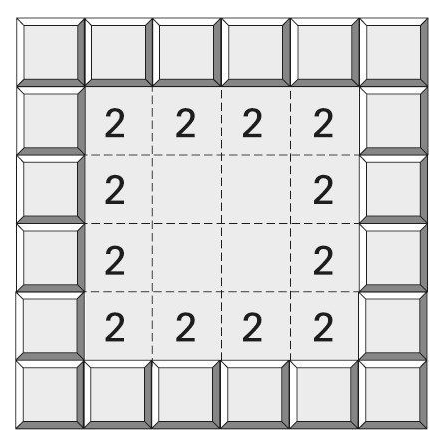
图　3-21

是否有一种布雷方式，能使数字是连续的呢？还是说以上图案完全不可能出自一个真实的游戏之中，因为不存在这种布雷方式呢？你要做的就是找出一种有效的程序，不管给出一幅什么样的画图，你都能给出答案。

数独

找到一种有效机制来完成任意大小的数独填字游戏也是一个NP完全问题。有时候，面对一些十分困难的数独问题时，我们必须要进行试探性的填写，然后沿着这些逻辑一点点填充下去。似乎并没有什么特别聪明的方法，我们只有一次一次地试探，直到找出一个准确的解决方法。

装箱问题

假设你经营一家搬家公司，公司中所有货箱的高度与宽度都是统一的，与货车车厢的内壁高度和宽度完全契合（仅略短一点，可以顺利塞入）。但货箱的长度各不相同。货车车厢的长度是150英尺，而货箱的长度则有以下几种规格：16、27、37、42、52、59、65及95英尺。

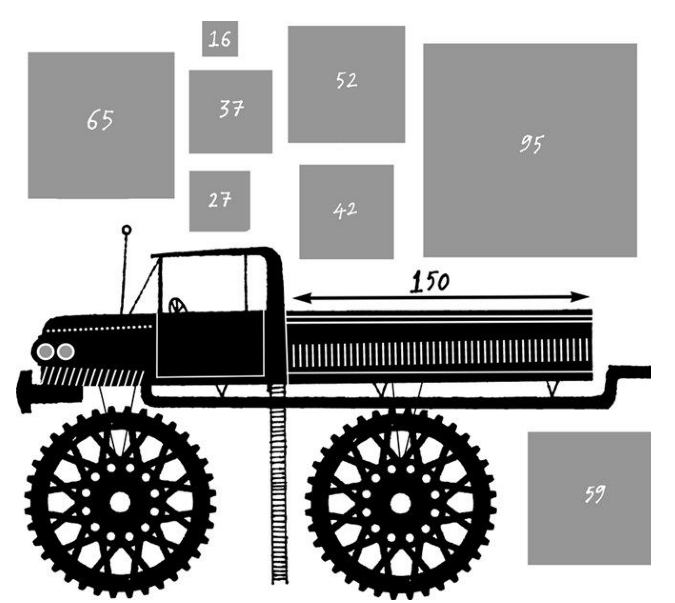
图 3-22　将货箱装车是一个复杂的数学问题

你能否找到一种最省空间的货箱装车方式呢？设定任意一个数字N 和一组更小的数字n (1)，n (2)，…，n (r )，你必须找到一种算法，以确定是否存在一种更小数字的组合方式，使其相加得出那个大数字？

这些问题并非仅仅是游戏而已，它们常出现在商业或产业之中，许多公司都需要找到一种有效方法去解决某个实际问题。空间或能源的浪费都会增加企业的运营成本，公司的管理者往往需要解决其中一个NP问题。甚至有一些电码也被应用在电信产业中，需要相关人员找到破解这些电码的秘密。总而言之，这些问题并非仅限于数学家或游戏玩家的圈子，这道百万难题也是和普通人息息相关的。

不管是从数学概率上分析足球联赛，还是筹办派对，不管是为地图上色，还是扫雷，这些都是本章这道百万难题的种种伪装，其中总会有某个版本能引起你的兴趣吧。但我还是有言在先：这道题或许看似有趣好玩，但它却是所有百万美元难题中最难解的。数学家认为，这些问题包含着某些本质上的复杂性，因此并不存在一种解决这些问题的快速方法。但麻烦在于，要证实某件东西为什么不存在总是比证实什么东西存在更加困难。不过，如果真想试图解决本章中的这道难题，你至少也会从中收获很多乐趣。