留名吉尼斯纪录大全有很多种疯狂手段。比如，一位意大利会计米歇尔·桑蒂利亚通过由后向前敲出64本书中的字母而创造了一项纪录（按照书籍的原始语言，共计3 361 851个单词，19 549 382个字母）。这些书籍包括《奥德赛》、《麦克白》、拉丁文圣经，以及2002年版的《世界吉尼斯纪录大全》。英国德比郡格罗索普的肯·爱德华则保持着1分钟吃掉最多蟑螂（36只）的世界纪录，而美国人阿什利塔·弗曼由于在12小时27分钟内踩着弹簧高跷跳了37.18公里的距离而跻身吉尼斯纪录。同时，弗曼还拥有保持最多项纪录的纪录！不过，数学能否帮助我们在吉尼斯的名人堂内斩获一席之地呢？

有一项吉尼斯纪录是看谁能够在最短时间内参观完伦敦地铁的所有车站，人们称之为地铁大挑战，吉尼斯纪录大全自1961年开始追踪这项纪录。当前的纪录是2009年12月14日由马丁·哈泽尔、史蒂文·威尔森及安迪·詹姆斯创下的，耗时6小时44分16秒。有人可能觉得这是一场十分辛苦的征程，但如果你想打破他们的记录，那么，对地铁线路图进行一番数学分析或许能帮你设计出一条最短的路程，它能保证你至少每个车站都经过一次。

地铁大挑战也并非横空出世，它实际上只是18世纪普鲁士哥尼斯堡人玩的一个游戏的复杂升级版。普雷格尔河的两条支流在向西流向波罗的海前会在哥尼斯堡城中心的小岛周围蜿蜒流过。18世纪时，普雷格尔河上共架有7座桥，当地人试图寻找一条路线，在一次行程中要通过所有桥，并且每座桥都只经过一次。这项活动逐渐演变为当地居民在周日午后的一项消遣。和地铁大挑战不同的是，该活动与速度无关，而是看谁能实现这样的一段行程。但是，不管人们如何努力尝试，却总是发现自己无法抵达其中的一座桥。难道这真是不可能完成的任务吗，还是确实存在某种可能的路径，只是他们还没发现呢？

这一问题最终由前文提到的瑞士数学家莱昂哈德·欧拉（他曾提出希腊拉丁幻方的问题）给出了答案，当时他正在哥尼斯堡东北500英里外的圣彼得堡的学院中执教。欧拉在一个十分重要的观念上实现了飞跃。他意识到，这个城市的实际尺寸在这个问题中是无关紧要的，重要的是桥梁之间是如何连接起来的（这个相同的原则也适用于伦敦地铁系统的拓扑地图）。被河流分割并由桥梁相连的四个区域均可浓缩为一个点，而那些桥梁则可以简化为连接这些点的线。由此得出的格尼斯堡桥梁地图看上去就像一个更加简化的伦敦地铁线路图（图3-13）。

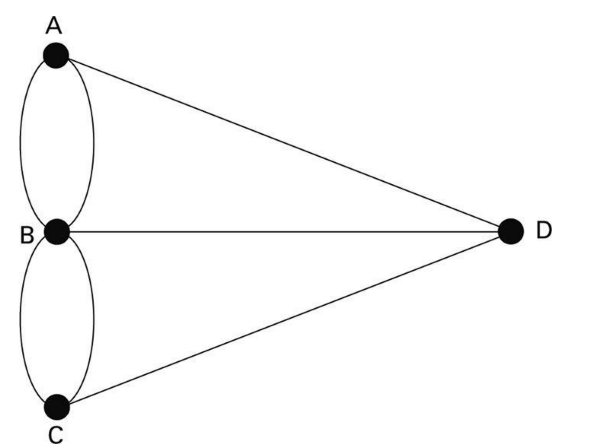
图　3-13

于是，能否在一次行程中走遍所有桥梁的问题，此刻就缩减成了能否用一支笔划过地图上的所有线条，同时避免在任何一条线上重复两次。欧拉发现，从这种新的数学角度来看，跨过所有7座桥梁，同时每座桥梁只经过一次，这一点的确是无法实现的。

原因何在呢？就像我们在地图上划线时一样，在途中经过每一个点时都必须有一条进入的线和一条离开的线。而如果再次造访同一个点，则需要通过一座新“桥梁”进入它，然后通过一座新“桥梁”离开它。因此，与每个点相连的线条数量必须是偶数才行，除行程的起始点和终结点以外。

我们再来看哥尼斯堡七座桥梁的地图，结果发现，其中的4个点都连接着奇数座桥梁，这也就意味着，我们不能找到一条路线能够连接所有的桥梁，且只经过每座桥梁一次。欧拉还做了进一步的分析。如果地图上刚好有两个点连接的直线数量为奇数的话，那么，要找到上述那样的路线则是可能的。要做到这一点，我们只要从其中一个连接奇数线条的点上出发，在另外一个连接奇数线条的点上结束即可。

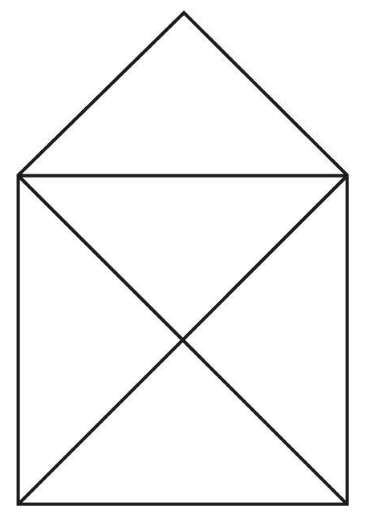
图 3-14　根据欧拉定理，我们可以用笔划过上述地图中的每一根线条，而且不会重复地划过任何一根线条

还有第二种类型的地图，也能够画出数学家们如今所称的欧拉路径：即每个点连接的线条数量均为偶数的地图。在这类地图上，你可以从任何一个点上开始，因为整个路径必须在同一个点上开始和结束，由此构成一个闭合的回路。尽管确认这样的一条路径或许困难重重，但根据欧拉定理，只要地图是上述描述的任何一种类型，便一定存在一条欧拉路径。这就是数学的强大力量所在：往往在我们并非必须构建它的时候，便可确保它的必然存在。

要证实这一路径的存在，我们可以从数学军火库中取出一件经典兵器——归纳法。这就像患有恐高症的我试图爬上一段高高的梯子或沿着绳索在瀑布中垂降时所做的那样：一次只迈一小步。(www.daowen.com)

请先想象一下，在某个地图上，你知道如何用笔划过一定数量的边，同时笔又不离开地图。但是，现在，你面对的地图比原来的多一边。此时，你是否依然能在新地图上画出欧拉路径呢？

假设，这个地图中有两个点A和B所连接的边数是奇数。这里的技巧就是先从其中一个连接奇数条边的点上去掉一条边。比如，我们把连接B与另一个点C之间的线条去掉。此时，在这个新地图上，仍然有两个点连接的线条数量为奇数，即A和C。（B点所连接的线条数已经变为偶数，因为我们刚刚从中移除了一条；而C连接的线条数变成了奇数，因为我们移除掉了连接C点与B点的那条线。）此时，这个新地图已变得足够小，只需从A点开始画起，至C点结束即可。经过这样的分析后，原先稍微复杂一点的地图也就迎刃而解了：只要把C点连接至B点即可，即把我们刚刚删掉的那根线补上便大功告成了！

我们需要分析其中的一些特殊情况。比如，如果连接B点和A点之间的线条只有一根，而A和C是同一点呢？不过我们可以看出，欧拉论证的核心便是这个美妙思路：一步一步摸着石头过河，以证明出为何欧拉路径是必然存在的。就像一步一步爬向梯子的高处，不管遇到多么大的一张地图，借助于这类技巧，我们总是可以慢慢地探索出一条道路。

为检验欧拉定理的强大之处，不妨请一位朋友画一幅尽可能复杂的地图。然后，先简单地数出所有连接奇数条边的点的数量，再根据欧拉定理，你就可以立即判断出该地图中是否存在这么一条欧拉路径。

最近，我前往哥尼斯堡朝圣，该市已在二战后被重新命名为加里宁格勒。经过盟军毁灭性的轰炸，这座城市的整个面貌已经完全不同于欧拉的那个时代了。不过，战前的所有桥梁中，还是有三座保留了下来，它们分别是木桥（Holzbrücke），甜蜜桥（Honigbrücke），以及高桥（Hühe brücke）。另外两座完全消失的桥梁是库特尔桥（Küttelbrücke）和铁匠桥（Schmiedebrücke）。剩下的两座桥绿桥（Grüne Brücke）和店主桥（Kramerbrücke）尽管也在战争中遭到损毁，但重建以后，已经成为这个城市中重要的双向通道。

此外，一座新的铁路桥（行人亦可使用）跨越普雷格尔河两岸，延伸至这个城市的西部，而一座新建的名叫凯撒桥的人行天桥则和旧高桥连接着相同的两个区域。作为一名数学家，我的立即反应就是能否追随18世纪的游戏精神，对今天的这些桥梁，展开一次贯穿之旅呢？

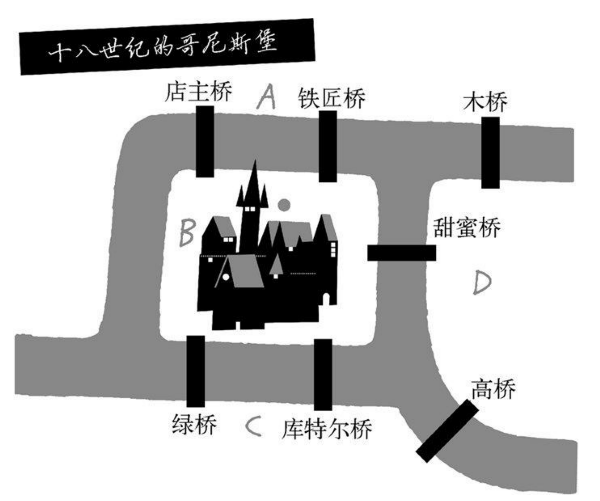
图 3-15　18世纪哥尼斯堡桥梁图示

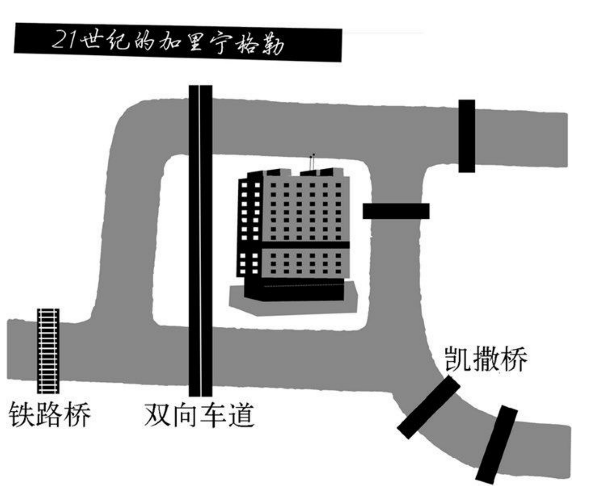
图 3-16　21世纪的加里宁格勒桥梁图示

根据欧拉的数学分析，只要刚好有2个区域所连接的桥梁数为奇数，那么便存在一条欧拉路径：我们只需从其中的一个区域开始，到另一个区域结束即可。通过察看今天的加里宁格勒的桥梁平面图，我发现像这样的一段行程事实上是可能存在的。

哥尼斯堡桥梁问题的意义十分重大，它为数学家带来了一种全新的看待几何与空间的方式。这个新的视角不再关注距离和角度，而专注于形状之间是以何种方式连接起来的。这便是拓扑学的起始点。拓扑学是过去几百年间最具影响力的数学分支之一，我们在第2章中已经做过介绍。由哥尼斯堡桥梁问题所引出的数学理论如今正应用在像谷歌这样的现代互联网搜索引擎中。这些搜索引擎寻求更多的导览网络的方式。此外，这些理论也有助于探索出地铁大挑战中最短的路径，如果你果真想尝试一下这项活动的话，不妨试试应用这些数学思想。