为庆祝法国大革命200周年，法国总统弗朗索瓦·密特朗请来丹麦建筑师约翰·奥托·凡·斯普雷克尔森在巴黎拉德芳斯的金融区打造一栋特别的建筑。这座建筑将加入卢浮宫、凯旋门及克丽欧佩特拉方尖碑这些巴黎重要建筑行列，成为所谓密特朗视野的一部分。

这位建筑师果然不负众望，建造了一座庞大的拱门，它被称为新凯旋门。该拱门庞大到连巴黎圣母院都能从中安然穿过，其重量高达30万吨。遗憾的是，斯普雷克尔森在拱门完工之前的两年便离开了人世。如今，新凯旋门已成为巴黎的标志性建筑之一，但是，那些整日目睹它的巴黎人可能并不了解，实际上，斯普雷克尔森在他们的首都市中心所建的正是一个四维立方体。

当然，它并非一个正儿八经的四维立体，毕竟我们生活在一个三维的世界中。不过，就像文艺复兴时期的艺术家面临着的在平整的二维帆布上绘制出三维形状那样的挑战，拉德芳斯区的这位建筑师也是一样，在我们的三维宇宙中捕捉到四维立体投射在三维宇宙中的幻影。要想在二维帆布上建立起三维幻景，艺术家可以在一个大正方形中画一个小正方形，然后将2个正方形的顶点连接起来以完成整个立方体的形状。当然，这样画出来的东西并非一个真实的立方体，但它向观看者传达出了足够多的信息：我们能看到所有立方体的边，因此便能想象出一个立方体的模样。

图 2-36　巴黎的新凯旋门是一个四维立方体的幻影

斯普雷克尔森借助于这个相同的想法，在三维的巴黎市中建造出了这座四维立方体的投影。这座建筑由一个大的立方体围绕一个小的立方体构成，2个立方体的顶点彼此相连构成四维立体的边。如果你有机会去新凯旋门参观并认真地数了其中边的数量，你就会总共数出32条边。这正是我们刚刚通过笛卡儿坐标所计算出的数字。

每次我去参观拉德芳斯区的新凯旋门时，总能感到那里有一阵阵可怕的阴风，通过中心的拱门仿佛要把人们吸进去一样。这种强风越来越成为一个问题，设计者不得不在拱门中心撑起一片天蓬，以阻碍空气的流动。这种强风似乎在向我们揭示，在巴黎建造这样一个超立体的幻影，便开启了一扇通往异度空间的大门。

在我们的三维世界中感受四维立体的存在还有一些其他方式。试想，我们如何能用1张二维卡片来制作出1个三维立体呢？首先，我们要画出6个彼此相连的正方形，构成一个十字架的结构，其中每一个正方形就是立方体的一个表面。然后再将其折叠起来，便可得到一个立方体。二维卡片于是被称为编织三维形状的“网”。同理，在我们的三维世界中也可以打造出一张三维网，只要第四维度果真存在，我们便可用这张网折叠出一个四维立体来。(www.daowen.com)

可以通过裁切和组装8个立方体的方式来创建出四维立体。这些立方体就是四维立体的“表面”。要做出四维立体的网，首先要把8个立方体连接起来。一开始，先把其中4个立方体首尾依次相连，粘成一列，再把其余的4个立方体分别粘在这个行列上的任何一个立方体的表面上。现在，折叠之前的超立方体便做成了，其形状就像两个组合起来的十字架（如图2-37所示）。

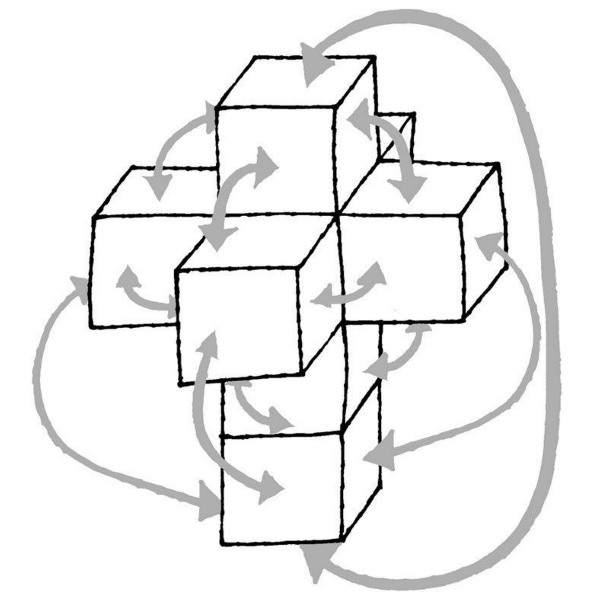
图 2-37　运用8个三维立方体创建出四维立方体的方法

要把这个形状折叠起来，首先你就要把这一列上的立方体的顶部和底部连接起来。然后，将这一列上粘着的2个相对的立方体向外的一面和这列中最下面的立方体向外的那一面连接起来，最后需要把立方体中的另外2个面和最下面的立方体剩余的2个面粘起来。当然，麻烦就是一旦开始进行拼接，你就会陷入混乱中，因为在我们的三维世界中，没有足够的空间让我们来完成这些工作。正如前文所说，首先要有一个四维空间，然后才能执行这个操作。

正像建筑师在巴黎的作品中受到四维立方体幻影的启发那样，艺术家萨尔瓦多·达利也受到这一组装前的超立方体概念的启发。在他的作品《耶稣受难》中，达利描绘出的耶稣被钉在一个四维立方体的三维编织网上。对达利来说，四维想法已超越了物质世界，是现实宇宙之外与精神世界发生共鸣的某种东西。未折叠的超立方体由2个交汇的十字架构成，画中的内容表示出耶稣的升天和尽力把三维结构折叠成四维形状相关，而在尽力的过程中，耶稣便超越了实体的现实。

不管我们如何努力试图在三维宇宙中描绘出这些四维形状，它们永远不可能提供一幅完整的图像，就像二维世界中的投影或轮廓那样，只能提供部分信息。当我们移动或旋转该立方体时，其阴影的形状也将发生变化，但是，我们永远无法窥其全貌。小说家亚历克斯·加兰在他的《四度空间》（The Tesseract）一书中便运用了这一思路。四度空间是四维四方体的另外一种说法。故事发生在马尼拉的黑社会中。作者分别从不同视角、不同人物描绘了中心故事。任何单一叙述都无法提供一幅完整图画，但通过把所有这些线索串联起来，就像通过观察一个形状中各个不同方向下的阴影一样，我们便可逐渐理解整个故事的完整面貌。不过，话说回来，第四维度的重要性并非只体现在建筑、绘画和叙事之中，它可能也是揭示宇宙本身形状的关键所在。