1960年，法国数学家本华·曼德博被邀请去哈佛大学经济系做一场讲座，介绍他近期研究的高收入和低收入之间的分布。在他踏入举办者的办公室后，看到黑板上竟然画着他为本次演讲而准备的图表时，感到心烦意乱。“你们是如何提前拿到我的数据的？”他问道。有趣的是，黑板上的图表和他要讲的收入问题毫不相关——它们其实是活动举办者在之前的一个讲座中分析的棉花价格走势。

这种相似性激发了曼德博的好奇心，他随后发现，一系列不相关的经济数据图表看起来都很相像。不仅如此，不管你看的是什么时间刻度的图表，它们的形状看上去都一样。比如，棉花价格在8年中的走势看上去和8周内的走势很像，也和8小时内的走势如出一辙。

同样的现象也存在于英国海岸线之中。以下面几幅图为例，这些都是苏格兰海岸线的片段。其中一幅的比例尺为1:1 000 000。另外两幅图相对不那么详细，比例尺分别为1:50 000和1:25 000。不过，你能因此判断出以下3张图分别对应的比例尺吗？不管你如何放大或缩小，这些线条似乎总保持同等程度的复杂性。这一点并不适用于任何形状。如果你弯弯曲曲地画一条线，然后将镜头拉近，放大其中的一段，当放大到一定程度后，整个线条就会变得非常简单。海岸线或者曼德博的图表的典型特征就是不管放大多少倍，其形状的复杂程度都一如既往。

随着曼德博研究范围的扩大，他便发现了这些奇怪的形状——即不管你如何放大这些形状，它们依旧保持着无穷的复杂性——遍布整个自然界。如果你从花菜上掰下一小块，然后将其放大，它看上去简直和整棵花菜如出一辙。如果你将曲折的闪电截取一段放大来看，它也不会呈现出一条直线，而是和原初的闪电形状别无二致。曼德博将这些分形体称之为“自然界的几何体”，因为它们代表着一种全新种类的形状，而且直到20世纪它们才首次被人类认知。

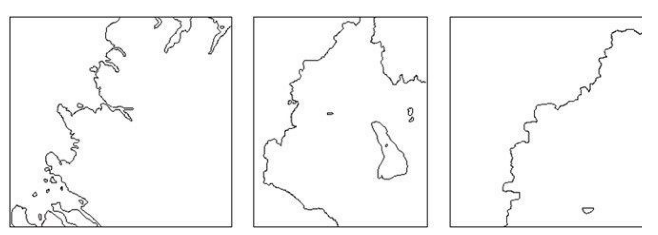
图 2-29　不同比例尺下的苏格兰海岸线。从左至右，比例尺依次为1:1 000 000，1:50 000和1:25 000(www.daowen.com)

自然界之所以能够创造出这些分形形状，是有着实际原因的。例如，人类肺部的分形形状就意味着，即使它置于胸腔的有限空间内，但其表面面积也可以十分巨大，因此可以吸入大量的氧气。同样的情况也存在于其他有机结构中。比如，蕨类植物能够最大范围地接触阳光，同时又不占据太多空间。它借助于自然的威力寻找出最有效的形状。正如气泡发现球体是最适合它们的形状那样，这些生命形式都选择了频谱的另一端，选择了具备无穷复杂性的分形形状。

最了不起的一点是，尽管这些分形具有无穷的复杂性，它们却是建立在非常简单的数学法则之上的。一开始我们可能很难相信，自然界中的复杂性竟会建立在简单的数学之上，但是，分形理论向我们揭示了，即使是自然界中最复杂的部分，也能通过简单的数学公式构建出来。

图2-30看上去像是蕨类植物的一片叶子，但是，实际上它只是电脑生成的一幅图像，所基于的只是一种类似于上文中创造科赫曲线时所使用的简单数学法则。IT界已经将该思路应用在了产业化中，用来创建电子游戏中复杂的自然背景。尽管一台主机的硬盘空间十分有限，但是，分形数学运算中的简单法则能帮助我们创建出纷繁复杂的背景环境。

图 2-30　分形体的蕨类植物