如果我们把柏拉图的5只足球中的某些顶点改造得更平滑，那么结果会如何呢？如果拿来1只二十面体的足球，将其每个顶点都削掉，那么，你应该会得到1只更圆的足球吧。在二十面体中，每个顶点都连接着5个三角形，将其削掉后，便会得到1个五边形。再把三角形的每个顶点都削掉后，其表面就会变成六边形，而最终得出的这个所谓的无顶二十面体，实际上就是1970年墨西哥世界杯决赛中首次使用的，而且现在仍在使用的当代足球形状。但是，是否能通过其他各种对称材料来为下届世界杯制作出一个更圆的足球呢？

公元前3世纪，希腊数学家阿基米德尝试改进柏拉图设计的足球形状。一开始，他选择使用两种或多种不同形状的原料来充当足球表面。由于每个表面都需要严丝合缝，因此每个表面的边长必须一模一样。只有这样，边与边之间才能做到完美对接。同时，他希望实现尽可能多的对称，因此每一个顶点——即面与面相遇的角——的形状也必须一模一样。如果2个三角形和2个正方形在其中的1个顶点相遇，那么，所有其他顶点的构造也必须如此。

阿基米德时时刻刻都沉浸在几何世界中。即使当他的仆人努力地把不情愿的阿基米德从数学世界中拉出来送去沐浴时，他依然会用手指蘸点儿烟囱的灰烬或油在光着的身子上画下几何图案。希腊历史学家普鲁塔克曾如此形容：“他在研究几何时所获得的愉悦使其忘记自我，从而陷入一种迷醉的境界。”

正是在这些几何禅定中，阿基米德才发现了对最佳足球形状的完整分类，并找到13种不同的方式，将这些形状组合起来。但是，阿基米德用来记录这些形状的手稿并没有保存下来。在500年后的亚历山大学派最后一位数学大师帕普斯的作品中，我们才看到有关这13种形状的发现的记录。这些形状被称为阿基米德立体（半正多面体）。

他创造的有些形状是通过修剪柏拉图的立体形状而得来的，制作过程和制作古典足球一样。比如，切掉四面体的4个顶点，原来的三角形表面就变成了六边形，而切割暴露出来的4个表面则变成4个新的三角形。因此，4个六边形和4个三角形组合起来便构成一个所谓的去顶四面体（如图2-5所示）。

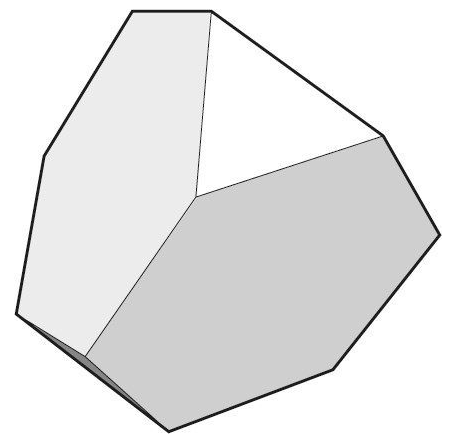
图　2-5

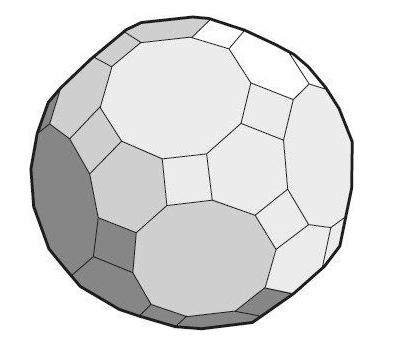
实际上，在13个阿基米德立体中，共有7个可以通过切割柏拉图的立体得出，包括由五边形和六边形所组成的经典足球。此外，更了不起的则是阿基米德还发现了其他形状。比如，可以将30个正方形、20个六边形和12个十边形组合起来构成一个匀称的球体，即伟大的小斜方截半二十面体（如图2-6所示）。

(www.daowen.com)

图　2-6

2006年德国世界杯首发的新型“时代精神”足球正是建立在其中的一款阿基米德立体之上的，这也是有史以来最圆的足球。这个由14个曲面材料所构成的足球的基本结构其实就是1个去顶八面体。把1个由8个等边三角形构成的八面体的6个顶点切掉后，原来的8个三角形就变成了六边形，而6个顶点则被6个正方形所取代（如图2-7所示）。

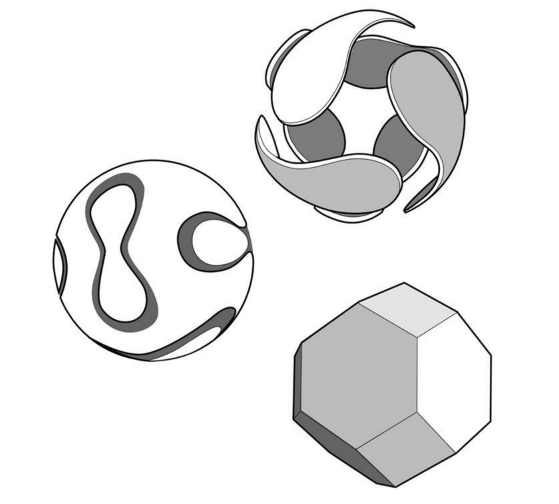
图　2-7

或许在以后的某届世界杯上，人们将推出阿基米德立体中一个更加奇异的形状。如果是我，我会选那个扭棱十二面体，该立体由92个对称组件（包括12个六边形和80个等边三角形）组合而成（如图2-8所示）。

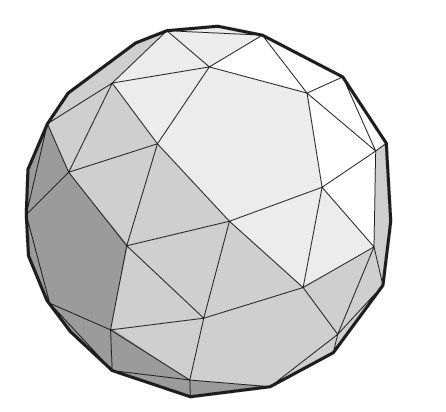
图　2-8

即使在生命的最后时刻，阿基米德惦记的也只有数学。公元前212年，罗马人入侵阿基米德的家乡锡拉库扎。阿基米德当时正全神贯注地求解一个数学难题，他聚精会神地画着图表，完全没有注意到他所在的这个城市已经沦陷。当一名罗马士兵挥着刀剑闯进他的房间时，阿基米德请求他，在杀他之前至少要让他完成眼下的运算。他哭着哀求道：“我怎么能留下半途而废的工作就离开人世呢？”显然这名士兵并没有足够的耐心等着他解开这个难题，直接了结了阿基米德的生命。