这是一个需要两位玩家参与的游戏，在玩游戏的过程中，如果对孪生质数有所了解，那么你的胜算几率会大增。

首先，依次写下100以内的数字，或从本书配套网站上下载质数跳房子游戏模板。第一位玩家先拿一颗筹码放在一个质数上，摆放的位置距离数字1的方格不可超过5步。下一位玩家要把一颗筹码放置在一个更大的质数上面，且距离玩家一摆放的位置不可超过5步。接下来第一位玩家照着做，并把筹码放到更大的质数上面，而且距离第二位玩家先前摆放的位置不可超过5步。无法根据规则走下一步棋的玩家便认输。游戏规则为：(1)筹码距离前面筹码的距离不得大于5步；(2)筹码必须放在质数上面；(3)筹码不能放着不动，也不能往反方向走。

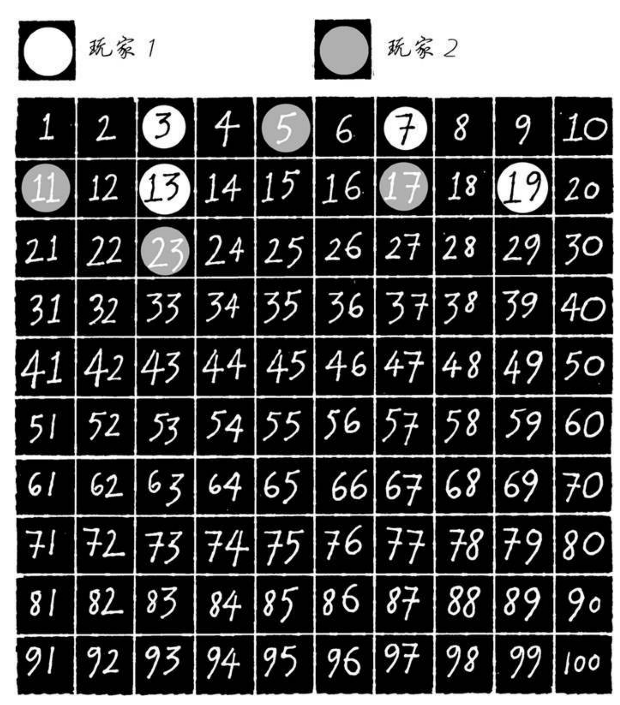
图 1-21　质数跳房子游戏案例，一次最多只能走5步

图1-21给出了一个典型的对战图。其中，第一位玩家输掉了比赛，因为下一位玩家的筹码放在质数23上，而23之后的5个数字都不是质数。那么，玩家1能否有一个更好的开局呢？如果你仔细观察上述局面，就会发现只要过了5这一关，后面也就没有多少选择了。谁能把筹码放在5上谁就是最后的赢家，因为在后面的一轮中，他将从19走到23，从而使对手下一步无棋可走。因此，开局是至关重要的。

我们不妨来修改一下游戏规则，玩家可以移动的最大步数从5步改为7步。现在，玩家可以跳得更远一点。特别的是，双方都可以顺利地通过23这个关口，从而可以把筹码放在6步之外的29上面。那么现在，开局依然重要吗？游戏将在哪里结束呢？亲自试验一下，你就会发现，这一次的选择要比刚才多多了，尤其是当你碰到一对孪生质数时。

初看之下，由于可走的棋路很多，似乎开局无关紧要。再仔细看一下，你就会发现，如果对手把筹码放在89的位置上，那么你便输掉了游戏，因为下一个质数一直要数到97才行，而97在89的8步以外。再回顾之前走过的棋，我们会发现，67后的这一步十分重要，因为，此时你面对的是两个孪生质数71和73，对于将筹码放在哪一个质数上面，需要作出选择。这一选择将决定游戏的输赢，因为此后的每一步都是别无选择的。不管哪位玩家把筹码放在67上，他都会赢，而89则似乎没那么重要。那么，你怎么能确保一定能把筹码放在67上呢？

继续回顾前面的棋路，结果我们发现，玩家在面对质数37的时候都要做出慎重的选择。37之后，你就要把筹码放在我两个女儿的“秘密中名”的孪生质数41和43上。如果你放在41上，你肯定就能拿下这场游戏。现在看来，谁能迫使对手把筹码放在37上，谁就能左右整个棋局。用这种方法继续向回看则会揭示出，这里的确存在一个决定输赢的开局。把筹码放在5上面，此后便能保证由你自己来面对所有上述的那些关键选择，进而确保把筹码放在89上面，使对手无路可走，从而赢得游戏。(www.daowen.com)

如果我们继续增加最多可以跳动的步数呢？游戏还是否一定能决出胜负呢？假如我们将最多跳动的步数定为99步，我们能确定游戏不会没完没了地进行下去吗？你总是可以在99步之内找到下一个质数来安放你的筹码吗？毕竟，大家都知道质数是无穷无尽的。因此，大概在某种情况下，你只要不停地从一个质数跳往下一个质数即可。

实际上，证明出游戏一定会结束这一点还是有可能的。不管你将最多跳跃步数设定成多大的一个数字，总会有比这个数字更大的一个范围，在其中找不到任何一个质数，这时，游戏便会终结。下面让我们来看如何找到99个非质数的连续数字。取数字100×99×98×97×…×3×2×1。这一数字称为100的阶乘，我们可以将其写为100!。接下来，我们要利用与该数字相关的一个重要事实：100!能够被从1到100之间的任何数字整除。

然后看下面的这组连续数字：

100!+2，100!+3，100!+4，…，100!+98，100!+99，100!+100

(100!+2)不是质数，因为它可以被2整除。同样，(100!+3)也不是质数，因为它能够被3整除。（100!能够被3整除，所以在此基础上加3，所得到的数字依然能够被3整除。）依此类推，以上所有数字皆非质数。比如(100!+53)，由于100!能被53整除，所以加上53后依然能被53整除。以上便是99个连续的非质数数字。我们之所以从(100!+2)开始，而没有从(100!+1)开始，是因为通过这个方法，只能推断出(100!+1)能被1整除，而这一点并不能帮助我们判断该数字是否为质数。（实际上它并不是。）

因此，我们可确定当最多跳跃数设为99时，该质数跳房子游戏还是会在某一位置上终结。不过，100!已经是一个巨大得不可思议的数字，实际上，在遇到这个数字之前游戏早就结束了：在质数396 733之后就能遇到首次连续99个非质数数字。

该游戏明显揭示了质数在数字世界中的分布是多么地飘忽不定。初看之下，我们无从知晓下个质数的位置所在。不过，若无法找到一种巧妙的方法，来帮助我们从一个质数寻索到下一个质数，那能否至少提出一些巧妙的公式来构造质数呢？